Question

Define refraction of light waves. Draw a ray diagram for refraction at a spherical separating two media. For refraction at a spherical surface, derive the relation $\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}} {u} = \dfrac{{{n_2} - {n_1}}}{R}$ in object distance $(u)$, image distance $(v)$ , refractive index of
media $({n_1},{n_2})$ and radius of curvature $(R)$.

Answer 1

Here we first draw the ray diagram correctly and label it. Then we assume the object distance, image distance and the radius of curvature and apply Snell’s law to get the answer.

Complete step by step answer:
If light rays enter a medium with different refractive index from another medium, they undergo a velocity transition. This is known as refraction of light. The velocity shift occurs in both the direction and amplitude of the light wave. Refraction of light is usually bending of light.

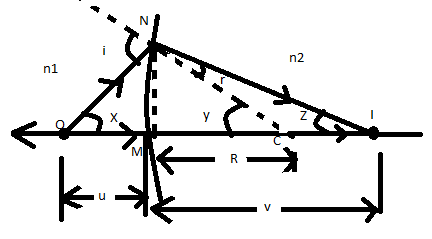
Now, let us consider $i$ and $r$ to be small.
Which means that $X,y,Z$ are small.
Also let $MN =$ length of arc, $OM \approx u$ is the object distance, $IM \approx V$ is the image distance and $CM \approx R$ is the radius.
Now,
From the figure we can observe that-
$i = X + y$ ...... (i)
$r = y - Z$ ...... (ii)
Using Snell’s law, we get-
${n_1}\sin i = {n_2}\sin r$

From equation (i) and (ii), we get-
${n_1}\sin (X + y) = {n_2}\sin (y - Z)$ ...... (iii)
Now let
$\sin (X + y) \approx X + y \approx \sin X + \sin y \\\ \sin (y - Z) \approx y - Z \approx \sin y - \sin Z \\\$

By using the sine formula we get-
$\sin X \approx \dfrac{{MN}} {u} \\\ \sin Z \approx \dfrac{{MN}} {v} \\\ \sin y \approx \dfrac{{MN}} {R} \\\$

Now, we can write equation (iii) as-
${n_1}\left( {\dfrac{{MN}}{u} + \dfrac{{MN}}{R}} \right) = {n_2}\left( {\dfrac{{MN}}{R} - \dfrac{{MN}}{v}} \right)$

Cancelling out $MN$
we get-
$\dfrac{{{n_1}}} {u} + \dfrac{{{n_2}}} {v} = \dfrac{{{n_2} - {n_1}}} {R}$

Applying the correct sign conventions, we get-
$u = - u \\\ v = + v \\\ R = + R \\\$

$\dfrac{{{n_2}}} {v} - \dfrac{{{n_1}}} {u} = \dfrac{{{n_2} - {n_1}}} {R}$

Hence, the relationship is derived

Additional Information:
Snell’s law- Snell’s law is a formula used when applied to light or other waves moving across a border between two different isotropic media, such as water, glass or air to explain the connection between the angles of incidence and refraction. Snell’s law is also known as the law of refraction.

Note:
Here since, the object is placed to the left of the mirror, so we take the object distance as negative. Also we have to carefully use the sine formula here; otherwise we shall not get the required derivation.