Question

Define principal focus of a convex lens. Draw a light ray diagram of an image formed, when the object is placed in between principal focus $F$ and $2F$.
Write lens formula.
Calculate power of a lens if its focal length is $0.5m$.

Answer 1

There are two focuses of a convex lens, the question is asking about principal focus, which is a point at which the object is put, unlike the secondary focus of the lens. To draw the ray diagram of an image formed, when the object is placed between $F$ and $2F$, consider two rays going through the lens, one from the optical center of the lens and the other going through the principal focus of the convex lens.
Lens formula is the same as mirror formula, just that the value of $f$ is different in the case of a lens and instead of summing on the LHS, we take the difference.
To find power, remember that power and focal lengths are reciprocal of each other, do consider the unit of focal length as well.

Complete step by step answer:
For convex and concave lenses, there are two focuses, Principal focus or primary focus and the secondary focus.
Primary or Principal focus is defined as the point on the principal axis of the lens at which if an object is placed, the image would be formed at infinity.
On the other hand, secondary focus of a lens can be defined as a point on which parallel rays after getting refracted from the lens converge at.
The ray diagram asked in the question is given below:

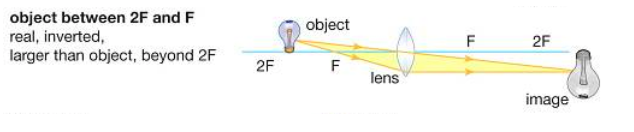
Now the question has asked us to write the lens formula, which can be written as:
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ or,
$\dfrac{1}{v} - \dfrac{1}{u} = \left( {{\mu _{rel}} - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Where, $v$ is the distance of image from the lens (with sign)
$u$ is the distance of the object from the lens (with sign)
${\mu _{rel}} = \dfrac{\mu }{{{\mu _m}}}$ where $\mu$ is the refractive index of the material of the lens and,
${\mu _m}$ is the refractive index of the medium in which the lens is put in
${R_1}$ is the radius of curvature of the first side which interacts with the light rays (with sign)
${R_2}$ is the radius of curvature of the other side (with sign).

Now for the last part of the question, we will use the formula:
$P = \dfrac{1}{f}$ where focal length is in meters.
Substituting the value given to us in the question:
$P = \dfrac{1}{{0.5}}\,D \\\ P = 2\,D \\\$

Hence, the power of the lens is two diopters.

Note: Many students get confused between the principal focus and secondary focus, so we have explained the difference in the solution very clearly. Other than that, which using the lens formula, many students do consider the relative refractive index and thus lose marks. Also, while using the formula of power of a lens, always check where the given focal length is in meters or not, if it is not in meters, convert it and then apply the formula.