Question
Question: Define mutual induction between a pair of coils. Derive an expression for the mutual inductance of t...
Define mutual induction between a pair of coils. Derive an expression for the mutual inductance of two long coaxial solenoids of same length wound one over the other.
Solution
If we place near each other and change the magnetic field of one coil, it will inspire electromagnetic changes to the other coil. This way the two coils reciprocate mutually. According to Faraday the electromagnetic changes in the second coil will try to oppose the change in magnetic field of the first coil.
Formula used:
EM=−dtdϕ
where EM is the EMF induced in the second coil, ϕ is the flux of magnetic field through the second coil.
Complete step by step answer:
Let us place two coils near each other and connect one coil to electrical supply that changes with time. Let’s say that the current flowing in this coil is I1. This coil can be called primary coil. As the current in the primary coil is changing, so, it will produce a magnetic field to oppose this change. Now, though the other coil is not connected to any supply, because it is kept near to the primary coil, the magnetic field lines of the primary coil will pass through it. Hence, there will be a changing magnetic flux inside the coil. Let us call this coil, the secondary coil. The secondary coil will try to oppose the changes in magnetic flux through it and that is why it will develop an electromotive force (EMF), which will oppose the changing magnetic flux by creating its own magnetic flux in direction opposite to the change. This way the secondary coil was inspired by the primary coil to develop EMF to oppose changes in magnetic field and thus this phenomenon is called mutual induction.
When two coils are placed near each other or brought near each other, the magnetic field of one coil gets linked to the other. This linking in the magnetic field leads to generation of voltage in the second coil called induced voltage. This is defined as mutual induction.
Let the lengths of the two coils be l and radius of the primary coil be r1 and that of secondary coil be r2. As both the solenoids are wound over each other, all the magnetic field lines of the primary coil pass through the secondary coil.
Let the number of turns in the primary coil be N1 and the number of turns in the secondary coil be N2.
If the current throughout primary coil is I1, the strength of at the axis magnetic field will be:
B1=lN1⋅μ0I1
As there are N1 turns in the coil, we multiplied N1 to the magnetic field of a single turn to get the total magnetic field. mu0 is the permeability of free space. For the secondary coil S2, this magnetic field exists only in the area occupied by the primary coil S1, which is πr12. Thus, the flux of magnetic field ϕ2 through secondary coil is:
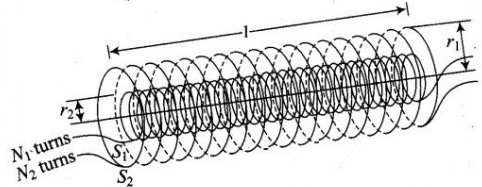
ϕ2&=N2⋅(lN1⋅μ0I1)πr12&=lμ0N1N2πr12I1=N2⋅B1⋅πr12
The induced EMF is given by Faraday’s Law:
EM&=−dtdlμ0N1N2πr12I1&=−lμ0N1N2πr12dtdI1&=−MdtdI1=−dtdϕ
M is called mutual inductance of the coils, given by the expression M=lμ0N1N2πr12.
Note:
The students may mistake the formula for magnetic field for an inductor as B=μnI with the one used above B=μ⋅lN⋅I. You should keep in mind that n is the number of turns per unit length and N is total turns of the coil. That is:
n=lN
