Question

Define intensity of the electric field at a point. Derive an expression for the electric field intensity due to a point charge.

Answer 1

Electric field intensity is described as the force experienced per unit positive charge on the very small positive test charge placed at that point. It is abbreviated as E. Electric field intensity is a vector quantity having both magnitude and direction.

Complete step by step answer:
First of all let us take a look at what an electric field intensity means. It is the space around an electric charge in which its influence can be experienced is known as the electric field. The electric field Intensity at a point is the force felt by a unit positive charge placed at that specific point. Basically electric field intensity is a vector quantity. It depends on both magnitude and direction. It is abbreviated as E. Unit of electric field is given as $N{{C}^{-1}}$or$V{{m}^{-1}}$. The electric field intensity results due to a positive charge which is always directed away from the charge and the intensity due to a negative charge is always directed towards the charge.

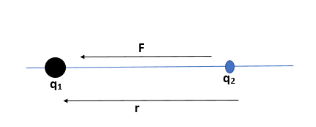
Let us take a point charge ${{q}_{2}}$ which is a unit test positive charge placed at a distance of $r$. Then according to the coulomb’s law, the force acting on the test charge will be given as,
$\overrightarrow{F}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}{{q}_{1}}{{q}_{2}}\dfrac{\left( \widehat{r} \right)}{{{r}^{2}}}$
Where${{q}_{1}}$ the charge resides there.
And also we know that the intensity of electric field at a given point is given by the equation,
$\overrightarrow{E}=\dfrac{\overrightarrow{F}}{{{q}_{2}}}$
Substituting the equation for force in this formula will give that,
$\overrightarrow{E}=\dfrac{\dfrac{1}{4\pi {{\varepsilon }_{0}}}{{q}_{1}}{{q}_{2}}\dfrac{\left( \widehat{r} \right)}{{{r}^{2}}}}{{{q}_{2}}}$
Cancelling the common terms and rearranging the terms will give,
$E=\dfrac{q}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}$
This is the intensity of the electric field at a distance r from the charge.
Hence the expression is derived.

Note:
The general difference between electric field and electric field intensity is that the electric field is the region around a charge in which it provides an electrostatic force on other charges. Field lines will not intersect each other. And they are perpendicular to the surface charge.