Question

Define impulse. State its S.I. unit. State and prove impulse-momentum theorem. A batsman deflects a ball by an angle of $45^{\circ}$ without changing its initial speed which is equal to $54 Km hr^{-1}$. What is the impulse imparted to the ball (Mass of the ball is $0.15$kg)?

Answer 1

Impulse can be described as the change in momentum of an object to which force is implemented. An object in the behaviour of any force accelerates or changes the velocity. The same force appearing on the same body for a long time will produce a more significant change in its linear momentum than the equivalent for a short duration.

Complete step by step answer:
Impulse defined as a force applied on an object for a short duration of time. Its S.I. unit is Ns. It is defined as the $1$ N force applied on a body for one second of time.
Impulse-momentum theorem states that Impulse applying on a body changes the same amount of linear momentum and change will occur in the same direction.
Proof: -
Let J is the impulse that produced between time $t_{1}$ and $t_{2}$.
F is the force acting in the time interval of $t_{1}$ and $t_{2}$.
We can write as –
$J =\int_{t_{1}}^{t_{2}} F dt$
By Newton’s second law, Force and momentum can related as-
$F = \dfrac{dp}{dt}$
$\implies J =\int_{t_{1}}^{t_{2}} \dfrac{dp}{dt} dt$
$\implies J =\int_{p_{1}}^{p_{2}} dp$
$\implies J=p_{2}-p_{1}$
Hence proved, impulse is equal to the change in linear momentum.
Given: - initial speed, u =$54 Km hr^{-1} = 54 \times \dfrac{5}{18} =15 m s^{-1}$
Initial speed is equal to final speed.
Mass of the ball = $0.15 Kg$
Ball is deviated at $45^{\circ}$ but the angle with the x-axis will be $22.5^{\circ}$.

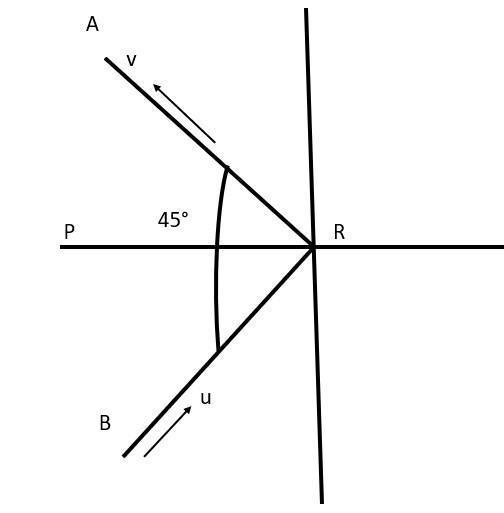
Initial momentum of ball = $mucos \theta$ along PR
Final momentum of ball = $mucos\theta$ along RP
$\text{ Impulse} = \text{Change in momentum}$
$J=2mucos\theta$
$\implies J= 2\times 0.15\times 15\times cos\theta$
$\implies J=4.16 Kg m s^{-1}$
$\therefore$ Impulse imparted to the ball = $4.16 Kg m s^{-1}$

Note: A small force acted for a long span will produce the same change in momentum as an Impulse force for a small duration. Forces which are acted over a short time interval are called impulsive forces. Impulse is a vector quantity. It arises basically during the collision.