Question

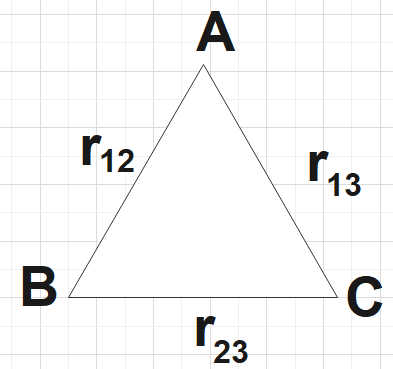
Define electrostatic potential at a point. Write its SI unit. Three charges ${{q}_{1}}$,${{q}_{2}}$ and ${{q}_{3}}$ are kept respectively at points A, B and C as shown in figures. Write the expression for electrostatic potential energy of the system.

Answer 1

You could first recall the definition and also the SI unit for electrostatic potential and then give the answer to that part. Then, you could recall the expression work done to bring charge to an arbitrary point and then work accordingly and hence find the answer, that is the net potential energy of the system.
Formula used:
Work done,
$w=qV=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}_{12}}}$

Complete answer:
In the question we are asked to define electrostatic potential at a point and give its SI unit. We are also given a system that contains three charges at the corners of a triangle and we are asked to find the system’s potential energy.
We could define potential energy at a point as the work done so as to bring a unit positive charge from infinity to some arbitrary point of consideration. The SI unit of electrostatic potential is known to be Volt. Let the position vectors of charges ${{q}_{1}}$,${{q}_{2}}$and ${{q}_{3}}$be$\overrightarrow{{{r}_{1}}}$,$\overrightarrow{{{r}_{2}}}$and $\overrightarrow{{{r}_{3}}}$respectively. Let the work done to bring ${{q}_{1}}$to $\overrightarrow{{{r}_{1}}}$be zero, then the work done to bring ${{q}_{2}}$to $\overrightarrow{{{r}_{2}}}$be,
${{w}_{2}}={{q}_{2}}{{V}_{1}}\left( \overrightarrow{{{r}_{2}}} \right)=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}_{12}}}$…………………………………… (1)
Now the work done to bring ${{q}_{2}}$to $\overrightarrow{{{r}_{2}}}$be,
${{w}_{3}}={{q}_{3}}{{V}_{1,2}}\left( \overrightarrow{{{r}_{3}}} \right)=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{{{q}_{1}}{{q}_{2}}}{{{r}_{12}}}+\dfrac{{{q}_{2}}{{q}_{3}}}{{{r}_{23}}} \right)$…………………………….. (2)
Now the net work done so as to arrange the given system would be the sum of (1) and (2) and this would get stored as potential energy. So, potential energy of the system would be,
$U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{{{q}_{1}}{{q}_{2}}}{{{r}_{12}}}+\dfrac{{{q}_{1}}{{q}_{3}}}{{{r}_{13}}}+\dfrac{{{q}_{2}}{{q}_{3}}}{{{r}_{23}}} \right)$

Note:
In case if you’re wondering why we have taken the work done to bring the first charge into the system zero. This is because we have assumed that all the three charges are brought one by one into the system. So, when the very first charge is brought there is no other charge in the system and hence the work done would be zero.