Question

Define electric flux. Apply Gauss' law to obtain an expression for the electric field intensity at a point due to an infinitely long uniformly charged straight wire. Draw the necessary diagram also.

Answer 1

Gauss law is applicable when there is a charged particle at rest or there is some well-defined charge distribution on a conductor.. Here we need to find a field due to an infinitely long conducting wire carrying linear charge density that is charged per unit length.

Complete step by step answer:
Electric flux is defined as the measure of flow of electric field through a given area. It is given as the dot product of electric field vector and the area vector.
${{\phi }_{E}}=\overrightarrow{E}.\overrightarrow{A}$
Electric flux is a scalar quantity.
Now, we need to find an expression for the electric field intensity at a point due to an infinitely long uniformly charged straight wire.
Let us assume there is an infinitely charged wire, having linear charge density $\lambda$. In order to find the electric field we assume a cylindrical gaussian surface as shown in the figure.

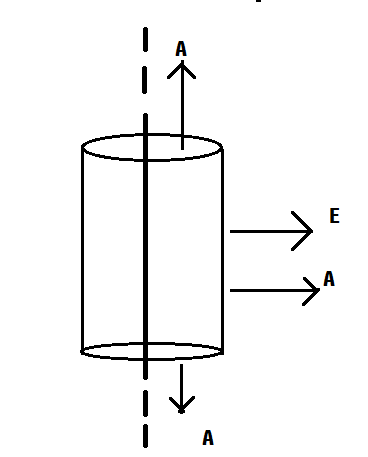
Applying gauss law, $\overrightarrow{E}.\overrightarrow{A}=\dfrac{{{Q}_{enc}}}{{{\varepsilon }_{0}}}$
First let us find the total charge enclosed by the gaussian surface. Let l be the length of the gaussian surface and let r be the radius.

& \lambda =\dfrac{q}{l} \\\ & q=\lambda l \\\ \end{aligned}$$ The lateral area vector and the electric field are parallel to each other and for curved surfaces one up and one down the angle between the electric field and the area vector are perpendicular. So, the only contribution comes from the lateral surface part. $$\overrightarrow{E}.\overrightarrow{A}=\dfrac{{{Q}_{enc}}}{{{\varepsilon }_{0}}}$$ $ \implies EA\cos 0=\dfrac{\lambda l}{{{\varepsilon }_{0}}} \\\ \implies E\times 2\pi rl=\dfrac{\lambda l}{{{\varepsilon }_{0}}} \\\ \therefore E=\dfrac{\lambda }{2\pi r{{\varepsilon }_{0}}} \\\ $ So the value of electric field intensity at a point due to an infinitely long uniformly charged straight wire comes out to be $$E=\dfrac{\lambda }{2\pi r{{\varepsilon }_{0}}}$$. **Note:** Had it been a case like a charge was situated inside the cube then we would have to apply gauss law to find the net flux through the cube. Gauss law states that the total flux through a closed surface is $$\dfrac{1}{\varepsilon }$$times the total charge inside that surface. Flux is given by the dot product of electric field vector and the area vector, since it involves dot product it is a scalar quantity.