Question

Define elastic collision. Show that in one dimensional elastic collision of two bodies, the relative velocity of separation after collision is equal to the relative velocity of approach before collision.

Answer 1

In any collision the linear momentum is conserved so the momentum before the collision and the momentum after the collision will be equal. Also in elastic collisions the kinetic energy is also conserved. So using these conditions the relation between the relative velocity of approach and relative velocity of separation can be calculated.
Formula used:
The momentum of a body of mass $m$ and velocity $v$ is
$p=mv$
And the kinetic energy is $K.E=\dfrac{1}{2}m{{v}^{2}}$

Complete answer:
A collision is said to occur between two bodies, either if they collide against each other or if the path of one is affected by the force exerted by the other. The collisions between the particles are of two types.
(1)Elastic Collision: If there is no loss of kinetic energy during a collision then the collision is called elastic collision. In elastic collision the kinetic energy and the momentum is conserved.
Examples: Collision between subatomic particles , collision between glass balls etc.
(2)Inelastic collision: If there is loss of kinetic energy during a collision then the collision is called inelastic collision. In inelastic collisions the kinetic energy is not conserved.
Examples: Collision between two vehicles, Collision between a ball and floor.
As shown in figure consider two perfectly elastic body A and B of masses ${{m}_{1}}$ and ${{m}_{2}}$ moving along the same straight line with velocities ${{u}_{1}}$ and ${{u}_{2}}$ respectively. Let ${{u}_{1}}>{{u}_{2}}$. After some times the two bodies collide head-on and continue to move in the same direction with velocities ${{v}_{1}}$ and ${{v}_{2}}$ respectively. The two bodies will separate after collision if ${{v}_{1}}>{{v}_{2}}$.

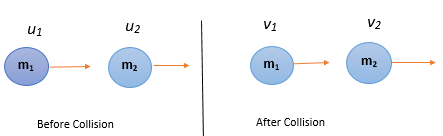
As the linear momentum is conserved in any collision so the linear momentum before the collision will be equal to linear momentum after the collision.
The linear momentum of A before the collision is ${{m}_{1}}{{u}_{1}}$
The linear momentum of B before the collision is ${{m}_{2}}{{u}_{2}}$
The linear momentum of A after the collision is ${{m}_{1}}{{v}_{1}}$
The linear momentum of B after the collision is ${{m}_{2}}{{v}_{2}}$
So according to conservation of linear momentum
$\begin{aligned} & {{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \\\ & \Rightarrow {{m}_{1}}{{u}_{1}}-{{m}_{1}}{{v}_{1}}={{m}_{2}}{{v}_{2}}-{{m}_{2}}{{u}_{2}} \\\ & \Rightarrow {{m}_{1}}\left( {{u}_{1}}-{{v}_{1}} \right)={{m}_{2}}\left( {{v}_{2}}-{{u}_{2}} \right) \\\ \end{aligned}$
Also the kinetic energy is conserved in elastic collisions. So
The kinetic energy of A before the collision is $\dfrac{1}{2}{{m}_{1}}u_{1}^{2}$
The kinetic energy of B before the collision is $\dfrac{1}{2}{{m}_{2}}u_{2}^{2}$
The kinetic energy of A after the collision is $\dfrac{1}{2}{{m}_{1}}v_{1}^{2}$
The kinetic energy of B after the collision is $\dfrac{1}{2}{{m}_{2}}v_{2}^{2}$
So according to conservation of linear momentum the kinetic energy before the collision is equal to the kinetic energy after the collision . so,
$\begin{aligned} & \dfrac{1}{2}{{m}_{1}}u_{1}^{2}+\dfrac{1}{2}{{m}_{2}}u_{2}^{2}=\dfrac{1}{2}{{m}_{1}}v_{1}^{2}+\dfrac{1}{2}{{m}_{2}}v_{2}^{2} \\\ & \Rightarrow {{m}_{1}}u_{1}^{2}-{{m}_{1}}v_{1}^{2}={{m}_{2}}v_{2}^{2}-{{m}_{2}}u_{2}^{2} \\\ & \Rightarrow {{m}_{1}}\left( u_{1}^{2}-v_{1}^{2} \right)={{m}_{2}}\left( v_{2}^{2}-u_{2}^{2} \right) \\\ & \Rightarrow {{m}_{1}}\left( {{u}_{1}}+{{v}_{1}} \right)\left( {{u}_{1}}-{{v}_{1}} \right)={{m}_{2}}\left( {{u}_{2}}+{{v}_{2}} \right)\left( {{u}_{2}}-{{v}_{2}} \right) \\\ \end{aligned}$
But from conservation of linear momentum we got
${{m}_{1}}\left( {{u}_{1}}-{{v}_{1}} \right)={{m}_{2}}\left( {{v}_{2}}-{{u}_{2}} \right)$
So dividing these two equations we get

& \dfrac{{{m}_{1}}\left( {{u}_{1}}+{{v}_{1}} \right)\left( {{u}_{1}}-{{v}_{1}} \right)}{{{m}_{1}}\left( {{u}_{1}}-{{v}_{1}} \right)}=\dfrac{{{m}_{2}}\left( {{u}_{2}}+{{v}_{2}} \right)\left( {{u}_{2}}-{{v}_{2}} \right)}{{{m}_{2}}\left( {{u}_{2}}-{{v}_{2}} \right)} \\\ & \Rightarrow \left( {{u}_{1}}+{{v}_{1}} \right)=\left( {{u}_{2}}+{{v}_{2}} \right) \\\ & \Rightarrow {{u}_{1}}-{{u}_{2}}={{v}_{1}}-{{v}_{2}} \\\ \end{aligned}$$ So the relative velocity of A with respect to B before the collision = Relative velocity of B with respect to A after the collision. Or this can also be said that the relative velocity of approach is equal to the relative velocity of separation. So this is proved that in one dimensional elastic collision of two bodies, the relative velocity of separation after collision is equal to the relative velocity of approach before collision. **Note:** When two bodies of equal masses suffer one dimensional elastic collision , their velocities will get exchanged. Also when an elastic body collides against another body of equal mass, initially at rest, after the collision the first body comes to rest while the second body moves with the initial velocity of the first. When a light body collides against a massive body at rest , the light body rebounds after the collision with equal, and opposite velocity while the massive body remains at rest..