Question

Define critical angle with reference to the total internal reflection. Calculate the critical angle for glass-air surface if a ray of light which is incident in air on the glass surface is deviated through ${15^ \circ }$, when angle of incidence is ${45^ \circ }$.

Answer 1

If a ray of light goes from a denser medium to rarer medium. There is a particular angle beyond which the light rays will no longer refract but will be reflected totally. This phenomenon is called total internal reflection.

Formula Used:
The angle beyond which light rays reflect totally is called the critical angle. It is denoted as ${i_c}$.
The relation between critical angle and refractive index of the medium is given as
$\sin \,{i_c} = \dfrac{1}{n}$
Where $n$ is the refractive index.
From Snell’s law we know that refractive index is the ratio of sine of angle of incidence to the sine of angle of refraction.
Therefore,
$n = \dfrac{{\sin \,i}}{{\sin \,r}}$ (2)
Where, $i$ is the angle of incidence and $r$ is the angle of refraction

Complete step by step answer:
If a ray of light goes from a denser medium to rarer medium. There is a particular angle beyond which the light rays will no longer refract but will be reflected totally. This phenomenon is called total internal reflection. The angle beyond which light rays reflect totally is called the critical angle. It is denoted as ${i_c}$.
The relation between critical angle and refractive index of the medium is given as
$\sin \,{i_c} = \dfrac{1}{n}$ (1)
Where $n$ is the refractive index.
From Snell’s law we know that refractive index is the ratio of sine of angle of incidence to the sine of angle of refraction.
Therefore,
$n = \dfrac{{\sin \,i}}{{\sin \,r}}$ (2)
Where, $i$ is the angle of incidence and $r$ is the angle of refraction

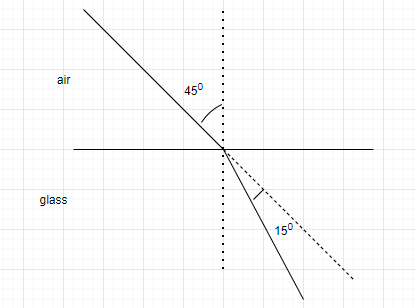
Given the angle of incidence is ${45^ \circ }$and the refracted ray is deviated by ${15^ \circ }$.
Observe the figure above.
This means the angle of refraction can be calculated as,
$r = {45^ \circ } - {15^ \circ } \\\ = {30^ \circ } \\\$
Substituting the value of $i$ and $r$ in equation (2)
We get,
Refractive index as
$n = \dfrac{{\sin \,{{45}^ \circ }}}{{\sin \,{{30}^ \circ }}} \\\ = \dfrac{{\dfrac{1}{{\sqrt 2 }}}}{{\dfrac{1}{2}}} \\\ = \sqrt 2 \\\$
Now using this value in equation 1 we get
$\sin \,{i_c} = \dfrac{1}{n} \\\ = \dfrac{1}{{\sqrt 2 }} \\\$
We need to find the angle ${i_c}$ therefore,
${i_c} = {\sin ^{ - 1}}\dfrac{1}{{\sqrt 2 }} \\\ = {45^ \circ } \\\$
Critical Angle for glass air interface is ${45^ \circ }$.

Note: It is important to note that in this question angle of deviation is given instead of angle of refraction, we need to subtract the deviation from angle of incidence to find the angle of refraction and only then use it in Snell's Law.