Question

Define Centripetal force.

Answer 1

A force that keeps a body moving in a circular path or curved path is known as Centripetal force. It is different from Centrifugal force. Centripetal force is an actual force, centrifugal force is defined as an apparent force. In other words, when twirling a mass on a string, the string exerts an inward centripetal force on the mass, while mass appears to exert an outward centrifugal force on the string.

Complete step-by-step solution:
Definition: Suppose a body is moving with a velocity V and if we apply a constant force F perpendicular to the velocity of that body then that body will begin to move in a curved path. That curved path will be a circle if the applied force F is constant and doesn’t change with time. Common examples are Whirling a stone tied to thread, the force of Earth’s gravity on the Moon, turning of a car ( Here the centripetal force is provided by the frictional force between the ground and the wheels.).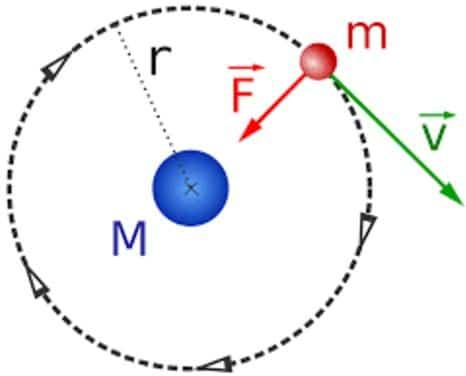

The expression to determine the applied force so that body having mass m moves in a circular path of radius r with a velocity v is given below
$F = \dfrac{{m{v^2}}}{r}$

Where:
F = Force to be applied
m = mass of the body
v = velocity the body
r = radius of the circle in which body is moving in circular motion

The direction of the force is towards the center in which the object is moving in a circular motion and F changes its direction every instant as the object changes its position and adjusts itself in such a way that its direction always remains towards the center.
From the given example of Earth and Moon we can easily calculate the velocity of the Moon
Let us calculate it
Given :
Earth’s mass = M
Moon’s mass = m
Gravitational force between two bodies = G.m1.m2/r.r
Distance between Earth and Moon = r
Applying concept that centripetal force is equal to gravitational force, on equating forces we get the below expression:
Gravitational Force equation :
$F = - \dfrac{{GmM}}{{{r^2}}}$
(- indicates that it is a attractive force )
Centripetal Force Equation:
$F = \dfrac{{m{v^2}}}{r}$

Equating them
$\dfrac{{GmM}}{{{r^2}}} = \dfrac{{m{v^2}}}{r}$
$v = \sqrt {\dfrac{{GM}}{r}}$

So here we get the velocity of the Moon with which it rotates around the moon.

Note:- For an object to maintain circular motion it must constantly change direction. Since velocity is a vector, changes in direction constitute changes in velocity. A change in velocity is known as an acceleration. The change in velocity due to circular motion is known as centripetal acceleration.