Question
Question: Define binding energy and obtain an expression of binding energy of a satellite revolving in a circu...
Define binding energy and obtain an expression of binding energy of a satellite revolving in a circular orbit around the earth.
Solution
Hint: In order to calculate the binding energy, we first need to find the total energy of the satellite (which is negative since it’s a bound system) and then find the additional amount of energy required to make it 0 i.e. its energy at infinity.
Complete step by step answer:
Binding energy is the minimum amount of energy required to free an object from a bound system and escape from its region of influence (i.e. escape to infinity). In the given case, it is the energy required by the satellite to leave its orbit around the earth and escape to infinity.
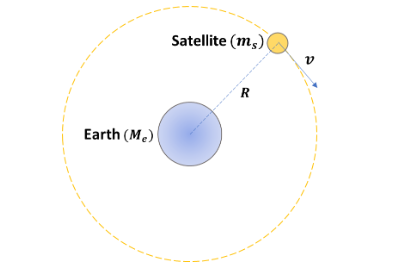
To begin, let us consider the earth-satellite system as given in the diagram below. The earth has a mass of Me and that of a satellite is ms. The distance between their center of masses is R. The satellite is moving at a speed of v in a fixed orbit.
Therefore, the kinetic energy (K) of the satellite is given by,
K=21msv2
Now, since it is in a stable circular orbit, the gravitational force must be equal to the centripetal force. Therefore,
Rmsv2=R2GMems
msv2=RGMems
Substituting the above value in K, we get,
K=21RGMems
And its potential energy (U) is given by,
U=∫∞RFdr
where F is the force felt by the satellite at a given distance r. It is given by,
F=r2GMems
Hence,
U=∫∞Rr2GMemsdr
U=−RGMems
Therefore, the total energy (E0) when in orbit is given by,
E0=K+U
E0=21RGMems−RGMems
E0=−21RGMems
Now, when the satellite escapes to infinity, we assume that it loses all its kinetic energy, and since it is at infinite distance from earth, its potential energy is zero. Therefore, its total energy at infinity (E∞) is given by,
E∞=0
Finally, the binding energy (B.E.) will be the difference of the two total energies, i.e.,
B.E.=E∞−E0
B.E.=21RGMems
Note:
The assumption of kinetic energy becoming zero after escaping to infinity is made to find the minimum binding energy. If it is asked that the object retains some velocity even at infinity, then the respective amount of kinetic energy must be added to the binding energy.
