Question

Define angle of repose. Prove that the coefficient of static friction is ‘tangent’ of the repose.

Answer 1

Hint: - Angle of repose is the minimum angle that an inclined plane makes with the horizontal plane when a body placed on it just begins to slide down. For the second part, you need to first make the free body diagram and mark the angle of repose and forces that will be acting on the block. This includes limiting friction, ${f_L}$, Normal force $N$, and the weight of the block $mg$. After equating all these forces in the form of an equation, use the formula for limiting friction and compare all the equations.

Formula used:
Limiting Friction, ${f_L} = \mu N$ where μ is the coefficient of friction, and $N$ is the normal force acting on the block.

Step-by-step solution:

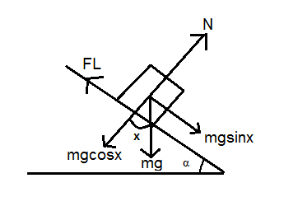
Make the diagram of the block as shown. $mg$ is the weight of the block acting vertically downward, $N$ is the normal force acting perpendicular to the diagonal surface of ramp, ${f_L}$ is the limiting friction acting in the opposite direction of motion of block along the diagonal surface of the ramp, $\alpha$ is the angle of repose, $mg\cos x$ and $mg\sin x$ are the respective components of force $mg$.
Now, we know that angle $\alpha$ will be equal to the angle $x$. Therefore,
$mg\cos x$ = $mg\cos \alpha$
$mg\sin x$ = $mg\sin \alpha$.
⇒ $N$ = $mg\cos \alpha$ (net force on a static object = 0) ------${\text{equation(1)}}$
Also, ${f_L}$ = $mg\sin \alpha$ (net force on a static object = 0)
We know that ${f_L} = \mu N$
Substituting the values of $N$ and ${f_L}$ in the above equation, we get, $mg\sin \alpha$ = $\mu N$
⇒ $mg\sin \alpha$ = $\mu$ × $mg\cos \alpha$ (using ${\text{equation(1)}}$)
On simplifying, we get,
$\sin \alpha$ = $\mu$ × $\cos \alpha$ ($mg$ gets canceled)
⇒ $\dfrac{{\sin \alpha }}{{\cos \alpha }} = \mu$ ⇒ $\tan \alpha = \mu$
Hence Proved.

Note: Make a free body diagram of the block to make calculations and force markings easier. It is important to mark the forces in proper directions in the free body diagram to make all our calculations correct otherwise the complete solution may go wrong.