Question

Define angle of friction and angle of repose. Show that angle of friction is equal to angle of repose for a rough inclined plane. A block of mass $4\,{\text{kg}}$ is resting on a rough horizontal plane and is about to move when a horizontal force of ${\text{30}}\,{\text{N}}$ is applied on it. If $g = 10{\text{m}}{{\text{s}}^{{\text{ - 2}}}}$. Find the total contact force exerted by the plane on the block.

Answer 1

There are three parts of the question, solve each part one by one. In the first part we are asked to define angle of friction and angle of repose for this, recall their definition. In the second part we are asked to prove that angle of friction is equal to angle of repose for this check for the common factor between the two so that you can relate them. In the third part solve the problem using the given quantities.

Complete step by step answer:
There are parts of the question, we will each part one by one.
Part I :- Angle of friction is the angle made by the normal force or reaction with the contact force when the condition of maximum static friction is reached or we can say it is the angle made by the resultant of the limiting friction and normal reaction with the normal reaction.Let us draw a figure to understand properly,

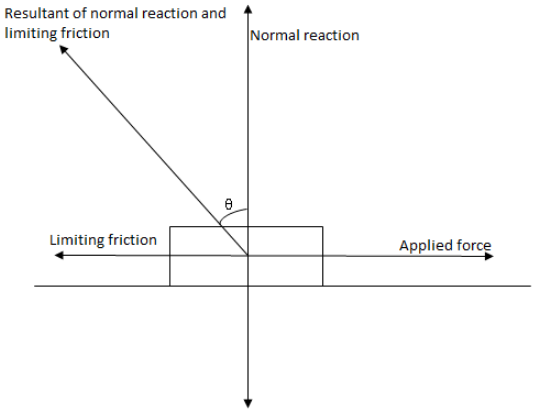
In the above figure $\theta$ is the angle of friction.

Angle of repose:- Angle of repose is the minimum angle made by the inclined plane with the horizontal when the body placed on it just begins to slide downwards.Let us draw a figure to understand properly,

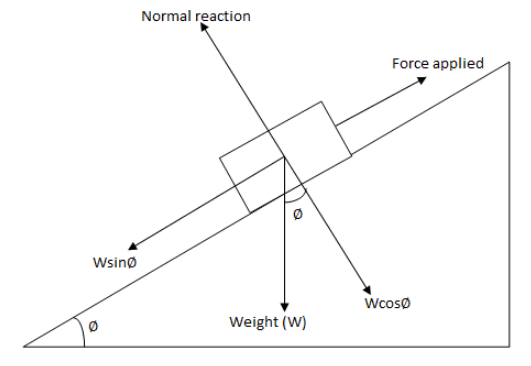
In the above figure $\phi$ is the angle of repose.

Part II :- We are asked to prove that angle of friction is equal to angle of repose for rough inclined planes.
The coefficient of static friction is defined as,
${\mu _s} = \tan \theta$ (i)
where $\theta$ is angle of friction
Coefficient of static friction can also be written as,
${\mu _s} = \tan \phi$ (ii)
where $\phi$ is angle of repose
Equating equations (i) and (ii), we get
$\tan \theta = \tan \phi$
Equating the angels we have,
$\theta = \phi$
Therefore, the angle of friction is equal to the angle of repose.

Part III:-
Given mass of a block, $m = 4{\text{kg}}$, Applied force, $F = 30{\text{N}}$
Acceleration due to gravity, $g = 10{\text{m}}{{\text{s}}^{{\text{ - 2}}}}$
We are asked to find the total contact force exerted by the plane on the block.The contact force or total force is the sum of all the forces. Apart from applied force, gravitational force will also be acting on the block downward and this force is written as,
${F_g} = mg$
Putting the values of $m$ and $g$ we have,
${F_g} = 4 \times 10$
$\Rightarrow {F_g} = 40{\text{N}}$
Therefore, contact force will be
${F_c} = {F_g} + F$
Putting the values of ${F_g}$ and $F$ we have,
${F_c} = 40 + 30$
$\therefore {F_c} = 70{\text{N}}$
Therefore contact force will be $70{\text{N}}$

Note: Most of the time students get confused between the definitions of angle of friction and angle of repose so carefully remember the difference between the two with the diagram. Remember that angle of friction is equal to angle of repose in the limiting friction.