Solveeit Logo
Login

Question

Question: Deduce the relation between n, u, v, R for refraction at a spherical surface, where the symbols have...

Deduce the relation between n, u, v, R for refraction at a spherical surface, where the symbols have their usual meaning.

Explanation

Solution

As a first step, you could make a neat ray diagram of a spherical surface. Then you could use simple geometry like the tangent of angles ⟨NIM\langle NIM and⟨NOM\langle NOM. Also, you could use Snell's law. Now, you will arrive at the required expression containing refractive index, image distance, object distance and radius of curvature.

Formula used:
Snell’s law,
n1sin⁡i=n2sin⁡r{{n}_{1}}\sin i={{n}_{2}}\sin r

Complete answer:
In the question, we are asked to deduce the relation between refractive index n, object distance u, image distance v and radius of curvature R of a spherical surface.

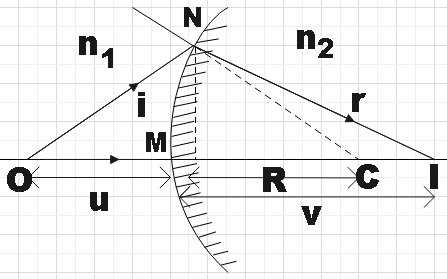
Let us consider a curved surface where the centre of curvature is C and the image of the object placed at O is formed at I. NM is perpendicular from point N to the principal axis.
We see that,
tan⁡⟨NOM≈⟨NOM=MNOM\tan \langle NOM\approx \langle NOM=\dfrac{MN}{OM}
Also,
tan⁡⟨NCM≈⟨NCM=MNMC\tan \langle NCM\approx \langle NCM=\dfrac{MN}{MC}
Similarly,
tan⁡⟨NIM≈⟨NIM=MNIM\tan \langle NIM\approx \langle NIM=\dfrac{MN}{IM}
Now, we have,
∴⟨i=⟨NOM+⟨NCM=MNOM+MNMC\therefore \langle i=\langle NOM+\langle NCM=\dfrac{MN}{OM}+\dfrac{MN}{MC}
Very similarly,
∴⟨r=⟨NCM−⟨NIM=MNMC−MNIM\therefore \langle r=\langle NCM-\langle NIM=\dfrac{MN}{MC}-\dfrac{MN}{IM}
On applying Snell’s law we have,
n1⟨i=n2⟨r{{n}_{1}}\langle i={{n}_{2}}\langle r
⇒n1MN(1OM+1MC)=n2MN(1MC−1I⁡M)\Rightarrow {{n}_{1}}MN\left( \dfrac{1}{OM}+\dfrac{1}{MC} \right)={{n}_{2}}MN\left( \dfrac{1}{MC}-\dfrac{1}{\operatorname{I}M} \right)
⇒n1OM+n2IM=n2−n1MC\Rightarrow \dfrac{{{n}_{1}}}{OM}+\dfrac{{{n}_{2}}}{IM}=\dfrac{{{n}_{2}}-{{n}_{1}}}{MC}
Now, we could apply the sign convention and also substitute the OM, IM and MC with v, u and R respectively to get,
n2v−n1u=n2−n1R\dfrac{{{n}_{2}}}{v}-\dfrac{{{n}_{1}}}{u}=\dfrac{{{n}_{2}}-{{n}_{1}}}{R}
Therefore, we found the final expression relating n, u, v, R for refraction at a spherical surface to be,
n2v−n1u=n2−n1R\dfrac{{{n}_{2}}}{v}-\dfrac{{{n}_{1}}}{u}=\dfrac{{{n}_{2}}-{{n}_{1}}}{R}

Note:
We have used the usual sign conventions while arriving at the final expression. We know that the distances when measured to the left of the optic axis are taken negative and distances measured to the right of the pole of the mirror are taken positive. So, u here is negative while R and v is positive.