Question

Date:

$(lim_{x \to 0.8} (Sinx) + (\frac{1}{n})^{Sinn} 43)$

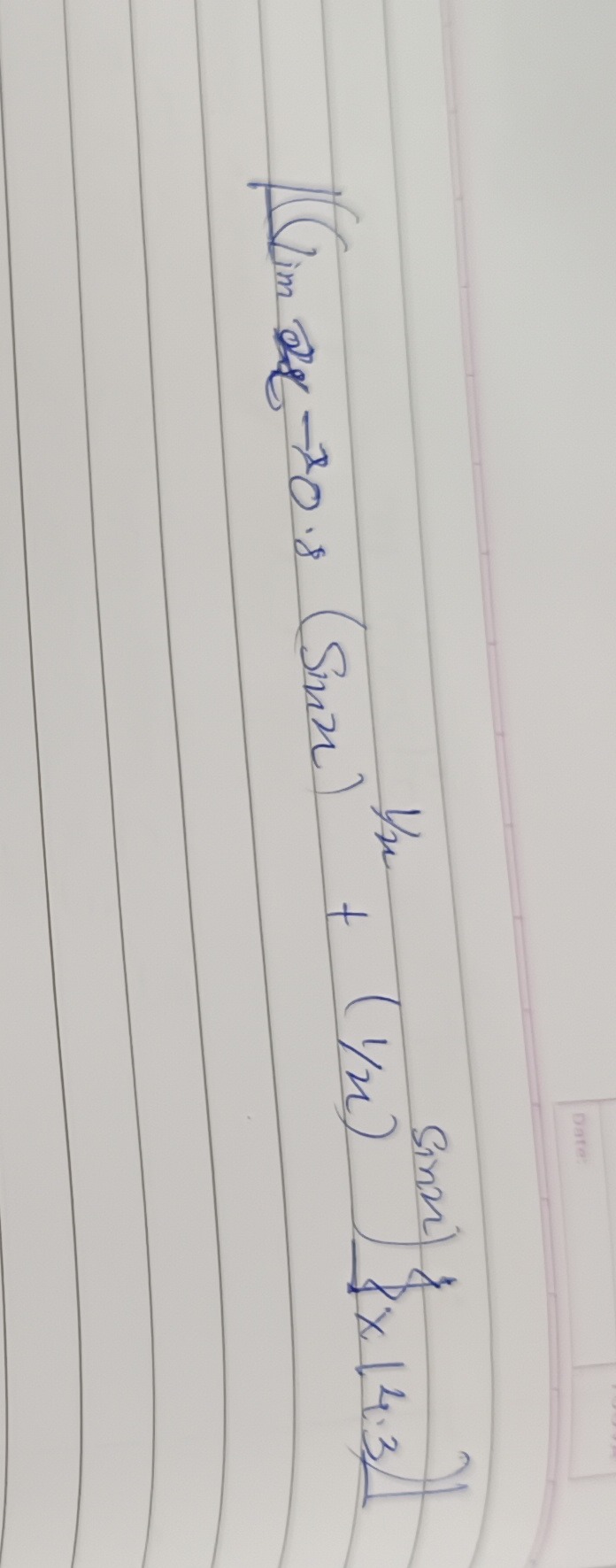
Answer 1

The overall limit is not defined (does not exist) because the second term does not have a limit.

Answer 2

Solution Explanation
The given expression is

$$\lim_{x\to0.8}\sin x + \left(\frac{1}{n}\right)^{\sin n}43.$$

Notice that there are two parts with different variables. The first limit

$$\lim_{x\to0.8}\sin x = \sin (0.8)$$

is straightforward. However, the second term, written as

$$\left(\frac{1}{n}\right)^{\sin n}43,$$

is ambiguous because:

1. It involves the variable $n$ but no limiting process for $n$ is stated.
2. Even if we assume a limit as $n\to\infty$, the exponent $\sin n$ oscillates between $-1$ and $1$. For instance, along a subsequence where $\sin n$ is close to $1$ the expression behaves like $\frac{43}{n}$ (tending to 0), while along another subsequence where $\sin n$ is close to $-1$ it behaves like $43\, n$ (diverging to $\infty$).

Thus, if one were to assume that the second term is meant to be evaluated as $n\to\infty$, it does not approach a unique value.

Answer
The overall limit is not defined (does not exist) because the second term does not have a limit.

Meta Information

• Subject: Mathematics
• Chapter: Limits and Derivatives
• Topic: Limit of a Function
• Difficulty Level: Medium
• Question Type: descriptive

Note: The expression is ambiguous due to mixing variables and unspecified limiting behavior for $n$. In an exam context, clarification of the intended limits is necessary.