Question

$d{{z}^{2}}$ orbital has :
(A) A lobe along the z-axis and a ring along xy-plane
(B) A lobe along the z-axis and a lobe along xy-plane
(C) A lobe along the z-axis and a ring along yz-plane
(D) A lobe and ring along the z-axis

Answer 1

Every orbital has a different shape and different lobes. The shape is decided by the azimuthal quantum number which is denoted as ‘l’. $d{{z}^{2}}$orbital is one of the 5 orbitals of d subshell which has a little different structure from ${{p}_{z}}$.

Complete step by step solution:
-There are 4 quantum numbers n, l, m and s. The principal quantum number (n) tells us about the shells of the atom. The azimuthal quantum number (l) tells us about the subshells of the atom. The magnetic quantum number (m) tells us about the orbitals of the atom and the spin quantum number (s) tells us about the orientation of the electrons in the orbital.
-Third quantum number is the magnetic quantum number and is denoted by m. It gives us the exact orbitals. Its total value can be given as ${{n}^{2}}$ or as (2l+1) since it lies in the range (-l to +l).
So, the d-subshell comes into picture when the value of n=3 and there are 5 orbitals for d-subshell since the value of l will be 2 for it. These orbitals are ${{d}_{xy}}, {{d}_{yz}}, {{d}_{xz}}, {{d}_{{{x}^{2}}-{{y}^{2}}, }}{{d}_{{{z}^{2}}}}$
-d-orbitals can be formed in 2 ways: between the axis and along the axis. $d{{z}^{2}}$ orbital is formed along the axis of the yz-plane and xz-plane. It has maximum electron density along the z-axis and is an axial orbital. The electron density of $d{{z}^{2}}$ orbital is negligible in the xy-plane and has the same phase in the opposite directions.

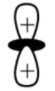
This is the shape of $d{{z}^{2}}$ orbital

So the correct option is A. A lobe along the z-axis and a ring along xy-plane.

Note: $d{{z}^{2}}$ orbital is similar to the ${{p}_{z}}$ orbital but is not the same. The probability of finding an electron is zero along the xy-plane for ${{p}_{z}}$orbital but this is not the case with the $d{{z}^{2}}$ orbital. Probability is not completely zero in it. Also, $d{{z}^{2}}$ orbital has the same phase in the opposite direction while ${{p}_{z}}$ orbital has a different phase in different directions.