Question
Question: A bead of mass m and diameter d is sliding back and forth with velocity V on a wire of length L held...
A bead of mass m and diameter d is sliding back and forth with velocity V on a wire of length L held between two rigid walls. Assume that the collisions with the wall are perfectly elastic and there is no friction. The average force that the bouncing bead exerts on the one of the wall is
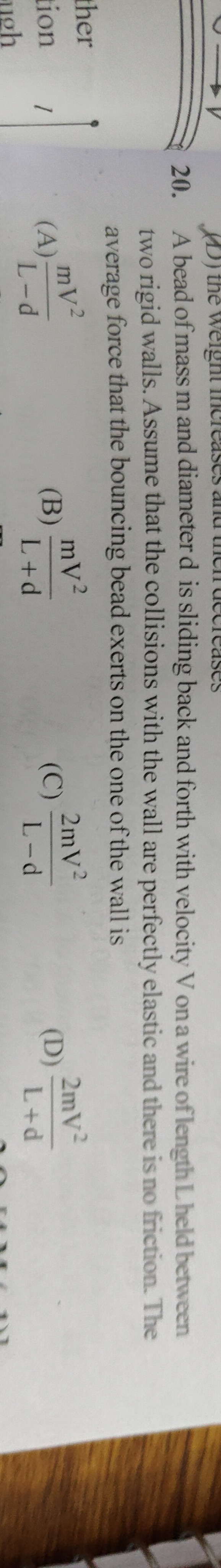
L−dmV2
L+dmV2
L−d2mV2
L+d2mV2
(A)
Solution
The problem asks for the average force exerted by a bead on one of the walls. We can solve this using the impulse-momentum theorem.
- Change in Momentum per collision:
When the bead collides with a wall, its velocity changes from V to -V (assuming perfectly elastic collision and reversal of direction).
The change in momentum of the bead (Δpbead) is:
Δpbead=m(−V)−m(V)=−2mV
By Newton's third law, the impulse exerted by the bead on the wall (which is equal to the change in momentum of the wall) has a magnitude of 2mV.
- Time between successive collisions with the same wall:
For the bead to collide with the same wall again, it must travel to the other wall and then return.
The effective length available for the bead's center of mass to travel between the two walls is L - d. This is because the bead has a diameter d, and its center cannot get closer than d/2 to either wall.
So, the distance traveled by the bead's center from one wall to the other is L - d.
The time taken for a one-way trip is tone_way=VL−d.
The time taken for a round trip (i.e., the time between two successive collisions with the same wall) is:
Δt=2×tone_way=V2(L−d)
- Average Force:
The average force exerted by the bead on the wall is the total impulse delivered to the wall over a time period, divided by that time period. In this case, it's the impulse per collision divided by the time between collisions with the same wall. Favg=Time between collisions with the same wallImpulse per collision Favg=V2(L−d)2mV Favg=2(L−d)2mV⋅V Favg=L−dmV2
The average force exerted by the bouncing bead on one of the walls is L−dmV2.
