Question

The incorrect statement is

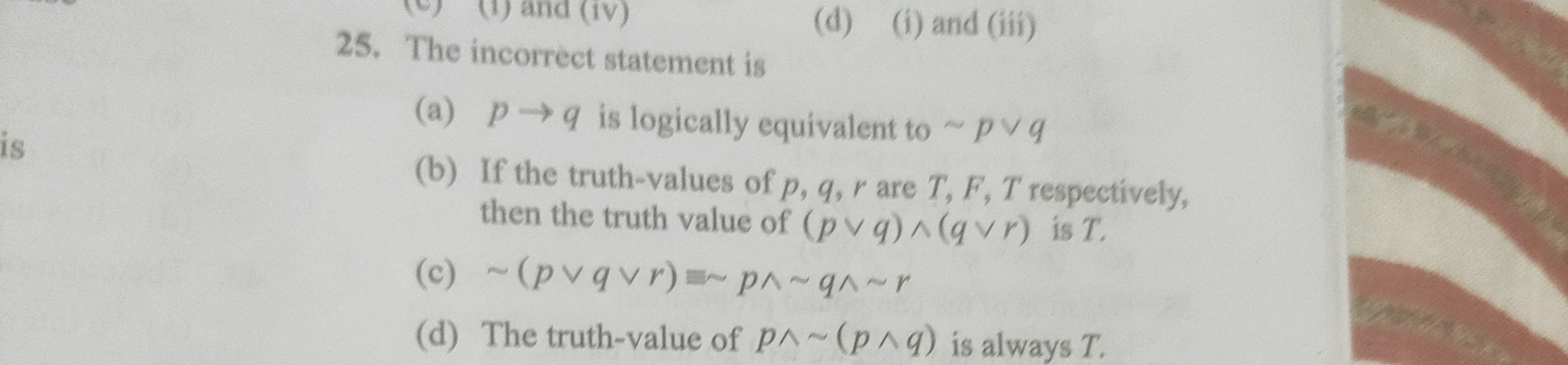
• A. $p \rightarrow q$ is logically equivalent to $\sim p \vee q$
• B. If the truth-values of $p, q, r$ are $T, F, T$ respectively, then the truth value of $(p \vee q) \wedge (q \vee r)$ is $T$.
• C. $\sim (p \vee q \vee r) \equiv \sim p \wedge \sim q \wedge \sim r$
• D. The truth-value of $p \wedge \sim (p \wedge q)$ is always $T$.

Answer 1

Answer: (D)

Option (d) is the incorrect statement.

Answer 2

We check each option:

1. Option (a):
   $p \rightarrow q \equiv \sim p \vee q$ is a standard logical equivalence. (Correct)

2. Option (b):
   Given $p = T, q = F, r = T$,
   $p \vee q = T \vee F = T$ and $q \vee r = F \vee T = T$.
   Hence, $(p \vee q) \wedge (q \vee r)= T \wedge T= T$. (Correct)

3. Option (c):
   By De Morgan's law,

   $$\sim (p \vee q \vee r) \equiv \sim p \wedge \sim q \wedge \sim r .$$

   (Correct)

4. Option (d):
   Evaluate $p \wedge \sim (p \wedge q)$.
   For $p = T$ and $q = T$:
   $p \wedge q = T$ hence $\sim (p \wedge q) = F$ and $T \wedge F = F$.
   Thus, its truth-value is not always $T$. (Incorrect)

Option (d) fails for $p=T, q=T$ since $p \wedge \sim(p \wedge q) = T \wedge F = F$.