Question
Question: Find value of Q from following equations. (i) C$_{(s)}$ + O$_{2(g)}$ $\longrightarrow$ CO$_{2(g)}$ ...
Find value of Q from following equations.
(i) C(s) + O2(g) ⟶ CO2(g) ΔH = QkJ (ii) C(s) + 21O2(g) ⟶ CO2(g) ΔH = -x kJ (iii) C(s) + 21O2(g) ⟶ CO2(g) ΔH = -y kJ
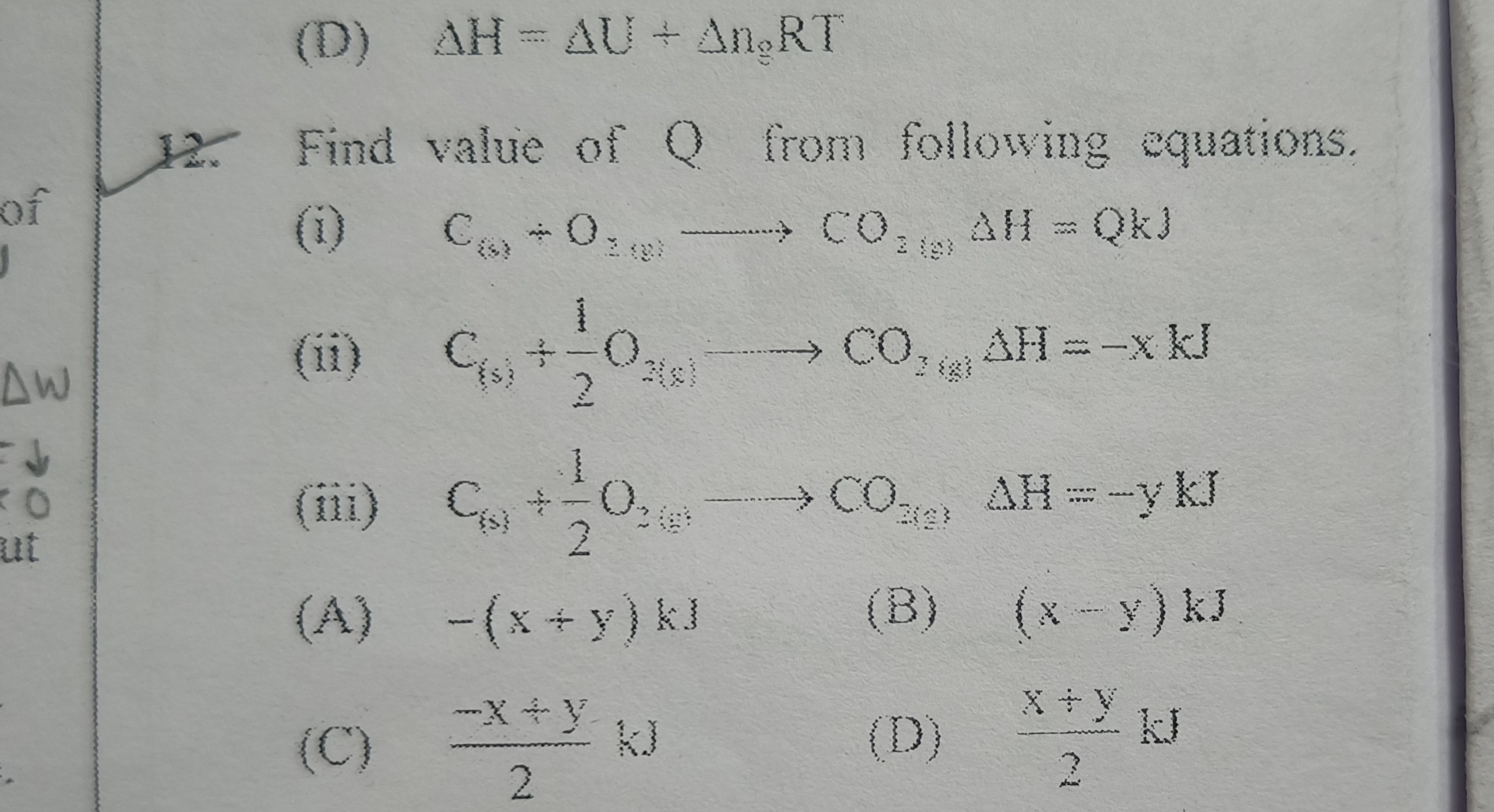
-(x + y) kJ
(x - y) kJ
2−x+y kJ
2x+y kJ
-(x + y) kJ
Solution
We note that the three equations refer to the formation of CO₂ from C and O₂ but written in “half‐reaction” form. In (ii) and (iii) the oxygen mole is ½; that is, they represent
C(s) + ½ O₂(g) → CO₂(g)
with measured energy changes –x kJ and –y kJ (the two experiments giving slightly different numbers because one measures ΔU while the other measures ΔH; recall that for an ideal‐gas reaction the two are related by
ΔH = ΔU + Δn₍g₎RT (1)
).
For the half‐reaction the number of moles of gas changes from ½ (reactant O₂) to 1 (product CO₂) so that Δn = 1 – ½ = ½. Thus one experimental result (say –x) represents the internal‐energy change ΔU while the other (–y) represents the enthalpy change ΔH. They are related by (1): (–y) = (–x) + ½RT ⇒ ½RT = (–y + x).
Now the “full” formation reaction is C(s) + O₂(g) → CO₂(g) (where Δn = 1–1 = 0 so that ΔH = ΔU). But since this reaction is just twice the half‐reaction we can “build it up” by “adding” an experiment on the half‐reaction obtained by bomb–calorimetry (giving –x kJ for ½ O₂) with that by constant–pressure calorimetry (giving –y kJ for ½ O₂). In other words the “true” value for the half–reaction may be taken as the average of the two measurements: Δ = ½[ (–x) + (–y) ] = –(x+y)/2. Then, to get the full reaction (which involves one mole of O₂ rather than ½), we must double the half–reaction so that the heat evolved becomes
Q = 2×[ –(x+y)/2 ] = –(x+y) kJ.
Thus the answer is Q = –(x+y) kJ.
Summary:
- Core explanation:
For the half–reaction C + ½O₂ → CO₂, one experiment yields –x kJ (ΔU) and the other –y kJ (ΔH). Their average is –(x+y)/2. But the full reaction (with 1 mole O₂) is exactly twice the half–reaction so Q = –(x+y) kJ.
