Solveeit Logo
Login

Question

Question: For any $1 \leq r \leq n-1$, the value of $^{n}C_r - 2 \cdot ^{n}C_{r-1} + 3 \cdot ^{n}C_{r-2} - 4 \...

For any 1≤r≤n−11 \leq r \leq n-1, the value of nCr−2⋅nCr−1+3⋅nCr−2−4⋅nCr−3+⋯+(−1)r(r+1)⋅nCr−r^{n}C_r - 2 \cdot ^{n}C_{r-1} + 3 \cdot ^{n}C_{r-2} - 4 \cdot ^{n}C_{r-3} + \dots + (-1)^r(r+1) \cdot ^{n}C_{r-r} is equal to

A

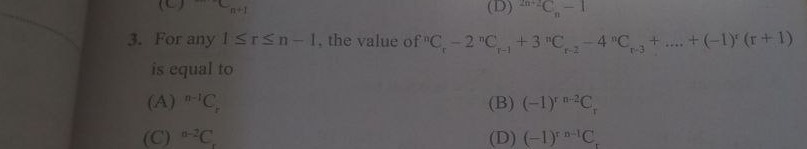
n−1Cr^{n-1}C_r

B

(−1)r⋅n−2Cr(-1)^r \cdot ^{n-2}C_r

C

n−2Cr^{n-2}C_r

D

(−1)r⋅n−1Cr(-1)^r \cdot ^{n-1}C_r

Answer

n−2Cr^{n-2}C_r

Explanation

Solution

Let the given series be SS. We can write it using summation notation as: S=∑k=0r(−1)k(k+1)(nr−k)S = \sum_{k=0}^{r} (-1)^k (k+1) \binom{n}{r-k}

Let j=r−kj = r-k. When k=0k=0, j=rj=r. When k=rk=r, j=0j=0. So k=r−jk = r-j. Substituting k=r−jk=r-j into the sum: S=∑j=0r(−1)r−j(r−j+1)(nj)S = \sum_{j=0}^{r} (-1)^{r-j} (r-j+1) \binom{n}{j} S=(−1)r∑j=0r(−1)−j(r−j+1)(nj)S = (-1)^r \sum_{j=0}^{r} (-1)^{-j} (r-j+1) \binom{n}{j} Since (−1)−j=(−1)j(-1)^{-j} = (-1)^j: S=(−1)r∑j=0r(−1)j(r−j+1)(nj)S = (-1)^r \sum_{j=0}^{r} (-1)^{j} (r-j+1) \binom{n}{j}

We can split the term (r−j+1)(r-j+1) into (r+1)(r+1) and −j-j: S=(−1)r[∑j=0r(−1)j(r+1)(nj)−∑j=0r(−1)jj(nj)]S = (-1)^r \left[ \sum_{j=0}^{r} (-1)^{j} (r+1) \binom{n}{j} - \sum_{j=0}^{r} (-1)^{j} j \binom{n}{j} \right] S=(−1)r[(r+1)∑j=0r(−1)j(nj)−∑j=0r(−1)jj(nj)]S = (-1)^r \left[ (r+1) \sum_{j=0}^{r} (-1)^{j} \binom{n}{j} - \sum_{j=0}^{r} (-1)^{j} j \binom{n}{j} \right]

We use the following identities for 1≤r≤n−11 \leq r \leq n-1:

  1. ∑j=0r(−1)j(nj)=(−1)r(n−1r)\sum_{j=0}^{r} (-1)^{j} \binom{n}{j} = (-1)^r \binom{n-1}{r}
  2. ∑j=0r(−1)jj(nj)=(−1)rn(n−2r−1)\sum_{j=0}^{r} (-1)^{j} j \binom{n}{j} = (-1)^r n \binom{n-2}{r-1}

Substituting these identities into the expression for SS: S=(−1)r[(r+1)(−1)r(n−1r)−(−1)rn(n−2r−1)]S = (-1)^r \left[ (r+1) (-1)^r \binom{n-1}{r} - (-1)^r n \binom{n-2}{r-1} \right] S=(r+1)(n−1r)−n(n−2r−1)S = (r+1) \binom{n-1}{r} - n \binom{n-2}{r-1}

Now we simplify this expression using binomial coefficient identities. We use the identity (Nk)=(N−1k)+(N−1k−1)\binom{N}{k} = \binom{N-1}{k} + \binom{N-1}{k-1}. (r+1)(n−1r)=(r+1)((n−2r)+(n−2r−1))(r+1) \binom{n-1}{r} = (r+1) \left( \binom{n-2}{r} + \binom{n-2}{r-1} \right) S=(r+1)(n−2r)+(r+1)(n−2r−1)−n(n−2r−1)S = (r+1) \binom{n-2}{r} + (r+1) \binom{n-2}{r-1} - n \binom{n-2}{r-1} S=(r+1)(n−2r)+(r+1−n)(n−2r−1)S = (r+1) \binom{n-2}{r} + (r+1-n) \binom{n-2}{r-1} S=(r+1)(n−2r)−(n−r−1)(n−2r−1)S = (r+1) \binom{n-2}{r} - (n-r-1) \binom{n-2}{r-1}

Consider the identity r(Nr)=N(N−1r−1)r \binom{N}{r} = N \binom{N-1}{r-1}. We want to show that S=(n−2r)S = \binom{n-2}{r}. If S=(n−2r)S = \binom{n-2}{r}, then we must have: (n−2r)=(r+1)(n−2r)−(n−r−1)(n−2r−1)\binom{n-2}{r} = (r+1) \binom{n-2}{r} - (n-r-1) \binom{n-2}{r-1} This implies: 0=r(n−2r)−(n−r−1)(n−2r−1)0 = r \binom{n-2}{r} - (n-r-1) \binom{n-2}{r-1} r(n−2r)=(n−r−1)(n−2r−1)r \binom{n-2}{r} = (n-r-1) \binom{n-2}{r-1}

Let's verify this identity: LHS: r(n−2r)=r(n−2)!r!(n−2−r)!=(n−2)!(r−1)!(n−2−r)!r \binom{n-2}{r} = r \frac{(n-2)!}{r!(n-2-r)!} = \frac{(n-2)!}{(r-1)!(n-2-r)!} RHS: (n−r−1)(n−2r−1)=(n−r−1)(n−2)!(r−1)!(n−2−(r−1))!=(n−r−1)(n−2)!(r−1)!(n−r−1)!(n-r-1) \binom{n-2}{r-1} = (n-r-1) \frac{(n-2)!}{(r-1)!(n-2-(r-1))!} = (n-r-1) \frac{(n-2)!}{(r-1)!(n-r-1)!} =(n−r−1)(n−2)!(r−1)!(n−r−1)(n−r−2)!=(n−2)!(r−1)!(n−r−2)!= (n-r-1) \frac{(n-2)!}{(r-1)!(n-r-1)(n-r-2)!} = \frac{(n-2)!}{(r-1)!(n-r-2)!} Since (n−2−r)!=(n−r−2)!(n-2-r)! = (n-r-2)!, the identity holds.

Therefore, S=(n−2r)S = \binom{n-2}{r}.