Question
Question: D(2,1,0), E(2,0,0), F(0,1,0) are midpoint of sides BC , CA, AB of \(\Delta ABC\) respectively, then ...
D(2,1,0), E(2,0,0), F(0,1,0) are midpoint of sides BC , CA, AB of ΔABC respectively, then the centroid of ΔABC is
A. (31,31,31)
B. (34,32,0)
C. (−31,31,31)
D. (32,31,31)
Solution
Hint: According to theorem centroid of triangle coincides with centroid of triangle formed by midpoint of sides of that triangle.
Complete step by step solution:
Coordinates of the midpoint of sides BC , CA, AB of triangle ABC are D(2,1,0), E(2,0,0), F(0,1,0) respectively.
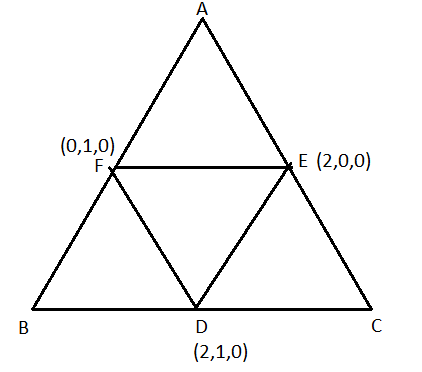
According to theorem centroid of triangle coincides with centroid of triangle formed by midpoint of sides of that triangle.
Hence the centroid of triangle ABC coincides with the centroid of triangle DEF.
If coordinates of vertices of triangle XYZ is X(x1,y1,z1),Y(x2,y2,z2),Z(x3,y3,z3) then coordinate of centroid of triangle XYZ is (3x1+x2+x3,3y1+y2+y3,3z1+z2+z3)
Hence centroid of triangle DEF is (32+2+0,31+0+1,30+0+0)=(34,32,0)
So centroid of triangle ABC is (34,32,0)
Hence option B is correct.
Note: In general if we say that two points coincide with each other it means the coordinates of those two points are the same in the coordinate system.
Also the centroid of the triangle is that point where medians of the triangle intersects each other.
