Question

If the vectors $(2i - qj + 3k)$ and $(4i-5j + 6k)$ are collinear then the value of q is

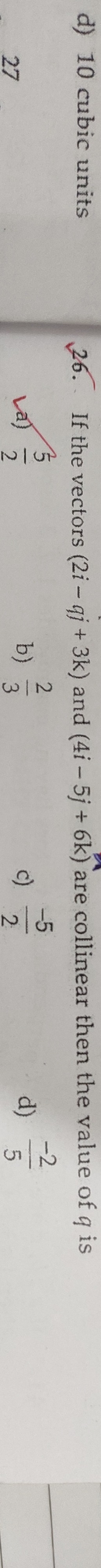
• A. $\frac{5}{2}$
• B. $\frac{2}{3}$
• C. $\frac{-5}{2}$
• D. $\frac{-2}{5}$

Answer 1

Answer: (A)

$\frac{5}{2}$

Answer 2

For the two vectors to be collinear, one must be a scalar multiple of the other. Assume

$$(2, -q, 3) = \lambda(4, -5, 6)$$

Comparing each component:

• $2 = 4\lambda \implies \lambda = \frac{1}{2}$
• $-q = -5\lambda \implies -q = -5\left(\frac{1}{2}\right) \implies q = \frac{5}{2}$
• $3 = 6\lambda \implies 3 = 6\left(\frac{1}{2}\right)$ (which is consistent)

Thus, the value of $q$ is $\frac{5}{2}$.