Question

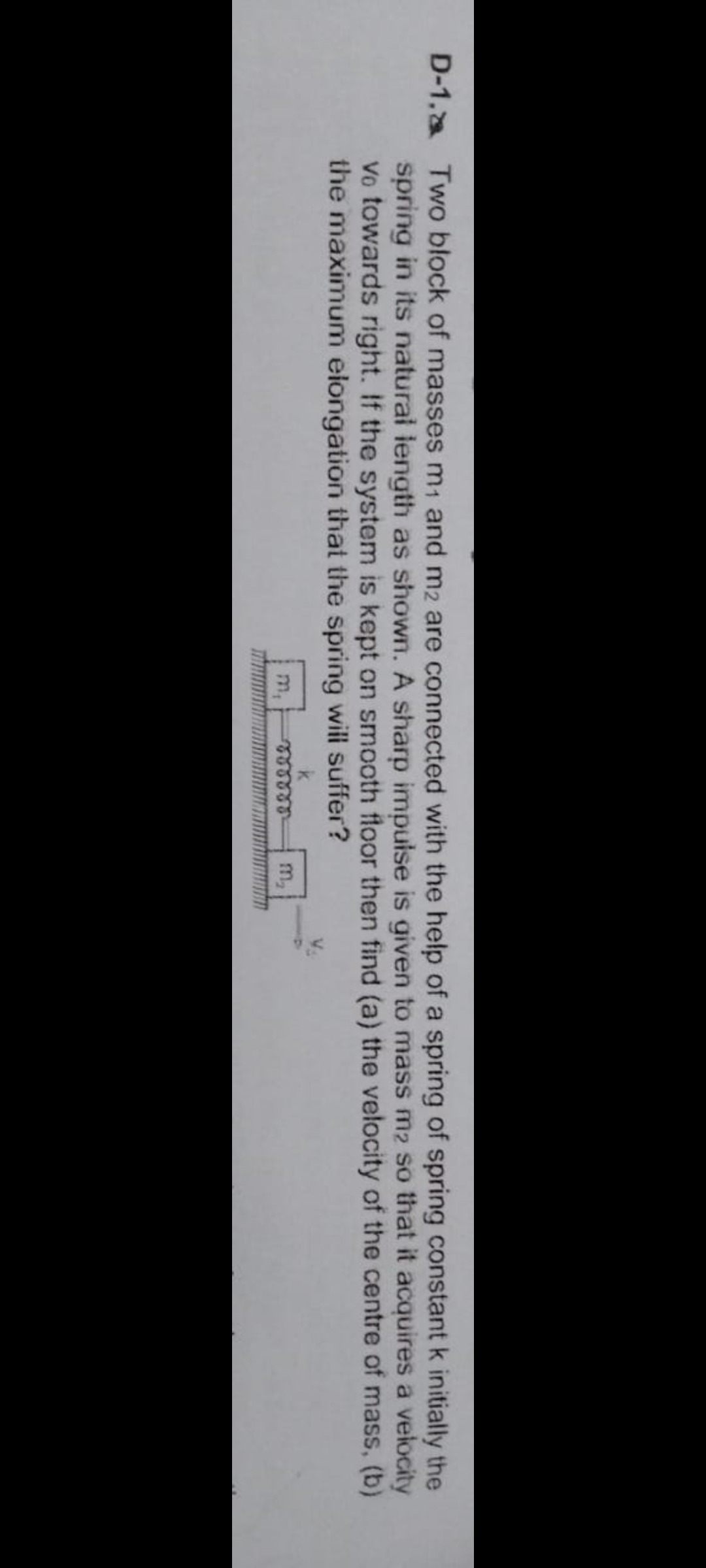
Two block of masses $m_1$ and $m_2$ are connected with the help of a spring of spring constant k initially the spring in its natural length as shown. A sharp impulse is given to mass $m_2$ so that it acquires a velocity $v_0$ towards right. If the system is kept on smooth floor then find (a) the velocity of the centre of mass, (b) the maximum elongation that the spring will suffer?

• A. (a) $\frac{m_2 v_0}{m_1+m_2}$, (b) $v_0\sqrt{\frac{m_1m_2}{k(m_1+m_2)}}$

Answer 1

Answer: (A)

(a) $\frac{m_2 v_0}{m_1+m_2}$, (b) $v_0\sqrt{\frac{m_1m_2}{k(m_1+m_2)}}$

Answer 2

The system consists of two blocks of masses $m_1$ and $m_2$ connected by a spring of spring constant $k$. The system is on a smooth floor. Initially, the spring is at its natural length. A sharp impulse is given to mass $m_2$ so that it acquires a velocity $v_0$ towards right.

(a) The velocity of the centre of mass:

The total external force on the system in the horizontal direction is zero after the initial impulse. Therefore, the total linear momentum of the system in the horizontal direction is conserved.

Before the impulse, both masses are at rest, so the initial total momentum is $P_i = m_1(0) + m_2(0) = 0$.

Immediately after the impulse, mass $m_1$ is still at rest ($v_1 = 0$) and mass $m_2$ has velocity $v_0$ ($v_2 = v_0$). The total momentum of the system immediately after the impulse is $P_f = m_1(0) + m_2(v_0) = m_2 v_0$.

The velocity of the centre of mass is given by $V_{CM} = \frac{P_{total}}{M_{total}}$, where $M_{total} = m_1 + m_2$.

Immediately after the impulse, the velocity of the centre of mass is $V_{CM} = \frac{m_2 v_0}{m_1 + m_2}$.

Since there are no external horizontal forces after the impulse, the velocity of the centre of mass remains constant.

Thus, the velocity of the centre of mass is $V_{CM} = \frac{m_2 v_0}{m_1 + m_2}$.

(b) The maximum elongation that the spring will suffer:

The maximum elongation of the spring occurs when the relative velocity between the two blocks is momentarily zero. At this moment, both blocks move with the same velocity. Since the velocity of the centre of mass is constant, this common velocity must be equal to the velocity of the centre of mass, $V_{CM}$.

We can use the conservation of energy. The total mechanical energy of the system (kinetic energy + potential energy of the spring) is conserved because the only force doing work after the impulse is the conservative spring force.

Let the initial state be immediately after the impulse, and the final state be when the spring has maximum elongation.

Initial state:

Velocity of $m_1$, $v_{1i} = 0$.

Velocity of $m_2$, $v_{2i} = v_0$.

Spring is at natural length, so potential energy $U_i = 0$.

Initial kinetic energy $K_i = \frac{1}{2} m_1 v_{1i}^2 + \frac{1}{2} m_2 v_{2i}^2 = \frac{1}{2} m_1 (0)^2 + \frac{1}{2} m_2 v_0^2 = \frac{1}{2} m_2 v_0^2$.

Total initial energy $E_i = K_i + U_i = \frac{1}{2} m_2 v_0^2$.

Final state (maximum elongation $x_{max}$):

Velocity of $m_1$, $v_{1f} = V_{CM} = \frac{m_2 v_0}{m_1 + m_2}$.

Velocity of $m_2$, $v_{2f} = V_{CM} = \frac{m_2 v_0}{m_1 + m_2}$.

Spring is elongated by $x_{max}$, so potential energy $U_f = \frac{1}{2} k x_{max}^2$.

Final kinetic energy $K_f = \frac{1}{2} m_1 v_{1f}^2 + \frac{1}{2} m_2 v_{2f}^2 = \frac{1}{2} m_1 \left(\frac{m_2 v_0}{m_1 + m_2}\right)^2 + \frac{1}{2} m_2 \left(\frac{m_2 v_0}{m_1 + m_2}\right)^2$.

$K_f = \frac{1}{2} (m_1 + m_2) \left(\frac{m_2 v_0}{m_1 + m_2}\right)^2 = \frac{1}{2} (m_1 + m_2) \frac{m_2^2 v_0^2}{(m_1 + m_2)^2} = \frac{1}{2} \frac{m_2^2 v_0^2}{m_1 + m_2}$.

Total final energy $E_f = K_f + U_f = \frac{1}{2} \frac{m_2^2 v_0^2}{m_1 + m_2} + \frac{1}{2} k x_{max}^2$.

By conservation of energy, $E_i = E_f$:

$\frac{1}{2} m_2 v_0^2 = \frac{1}{2} \frac{m_2^2 v_0^2}{m_1 + m_2} + \frac{1}{2} k x_{max}^2$.

$m_2 v_0^2 = \frac{m_2^2 v_0^2}{m_1 + m_2} + k x_{max}^2$.

$k x_{max}^2 = m_2 v_0^2 - \frac{m_2^2 v_0^2}{m_1 + m_2} = m_2 v_0^2 \left(1 - \frac{m_2}{m_1 + m_2}\right) = m_2 v_0^2 \left(\frac{m_1 + m_2 - m_2}{m_1 + m_2}\right) = m_2 v_0^2 \left(\frac{m_1}{m_1 + m_2}\right) = \frac{m_1 m_2}{m_1 + m_2} v_0^2$.

$x_{max}^2 = \frac{m_1 m_2}{k(m_1 + m_2)} v_0^2$.

$x_{max} = v_0 \sqrt{\frac{m_1 m_2}{k(m_1 + m_2)}}$.

Alternatively, using relative motion and reduced mass $\mu = \frac{m_1 m_2}{m_1 + m_2}$:

The initial kinetic energy of relative motion is $K_{reli} = \frac{1}{2} \mu v_{reli}^2$, where $v_{reli} = v_{2i} - v_{1i} = v_0 - 0 = v_0$.

$K_{reli} = \frac{1}{2} \mu v_0^2 = \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} v_0^2$.

At maximum elongation, the relative velocity is $v_{relf} = 0$, so $K_{relf} = 0$.

The initial potential energy of the spring is $U_i = 0$.

The final potential energy of the spring is $U_f = \frac{1}{2} k x_{max}^2$.

The energy associated with the relative motion and spring potential energy is conserved: $K_{reli} + U_i = K_{relf} + U_f$.

$\frac{1}{2} \mu v_0^2 + 0 = 0 + \frac{1}{2} k x_{max}^2$.

$\frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} v_0^2 = \frac{1}{2} k x_{max}^2$.

$x_{max}^2 = \frac{m_1 m_2}{k(m_1 + m_2)} v_0^2$.

$x_{max} = v_0 \sqrt{\frac{m_1 m_2}{k(m_1 + m_2)}}$.