Question

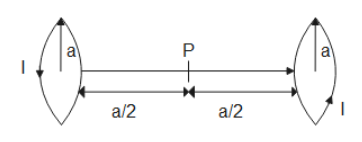
Currently both coils are flowing in an anti-clockwise direction when seen from the eye. Calculate the magnetic field intensity at point P.

Answer 1

Charges at rest produce only electric fields while charges in motion produce both electric and magnetic fields. Current is flowing through wire means that charge is in motion which produces the magnetic field and we will calculate the magnetic field produced by it at the required point
Formula used:
$B = \dfrac{{{\mu _0}i{r^2}}}{{2{{\left( {{r^2} + {x^2}} \right)}^{\dfrac{3}{2}}}}}$

Complete answer:
Electricity and magnetism are interdependent on each other. Motion of the magnet in the conducting loop generates the eddy currents while motion of charge in the conductor produces the magnetic field around it.
Here current is flowing in the coils in the same direction. So a magnetic field will be produced at point P due to both the coils. From the diagram below we can clearly understand that

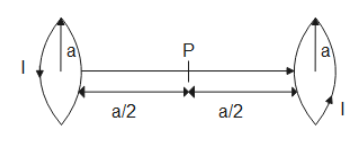
We have a formula to find out the magnetic field on any point on the axis of the loop.
That formula is $B = \dfrac{{{\mu _0}i{r^2}}}{{2{{\left( {{r^2} + {x^2}} \right)}^{\dfrac{3}{2}}}}}$ where ${\mu _0}$ is the permeability in free space and equal to $4\pi \times {10^{ - 7}}$ and ’i’ is the current and equal to I amperes and ‘r’ is the radius which was already given as ‘a’ and ‘x’ is the axial distance from the center of the circular loop which is given as 0.5a. By substituting all these values in the formula we get
\eqalign{ & B = \dfrac{{{\mu _0}i{r^2}}}{{2{{\left( {{r^2} + {x^2}} \right)}^{\dfrac{3}{2}}}}} \cr & \Rightarrow B = \dfrac{{{\mu _0}I{a^2}}}{{2{{\left( {{a^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} \right)}^{\dfrac{3}{2}}}}} \cr & \therefore B = \dfrac{{4{\mu _0}I}}{{5\sqrt 5 a}} \cr}
If we curl our right hand along the circular path of flow of current in circular lire then along the thumb we will get the direction of the magnetic field at a point on the axis of the loop.
So the magnetic fields at the point P due to two loops will be in same direction that is along the positive x axis i.e right side
So magnetic fields due to two loops will add and the resultant magnetic field will become
\eqalign{ & B = \dfrac{{4{\mu _0}I}}{{5\sqrt 5 a}} \cr & \Rightarrow {B_{result}} = 2 \times \left( {\dfrac{{4{\mu _0}I}}{{5\sqrt 5 a}}} \right) \cr & \therefore {B_{result}} = \dfrac{{8{\mu _0}I}}{{5\sqrt 5 a}} \cr}
Hence the resultant magnetic field at P will be $\dfrac{{8{\mu _0}I}}{{5\sqrt 5 a}}$

Note:
From the given question, if we change the direction of any of one current then the resultant magnetic field will be zero. They will cancel out. Magnitude will be the same in both the cases, but the direction will be varying. We can find the direction of the magnetic field anywhere on the axis by using the formula we have.