Question
Question: Current through \(100\Omega \) resistor is (Given forward resistance of diode = \(50\Omega \), re...
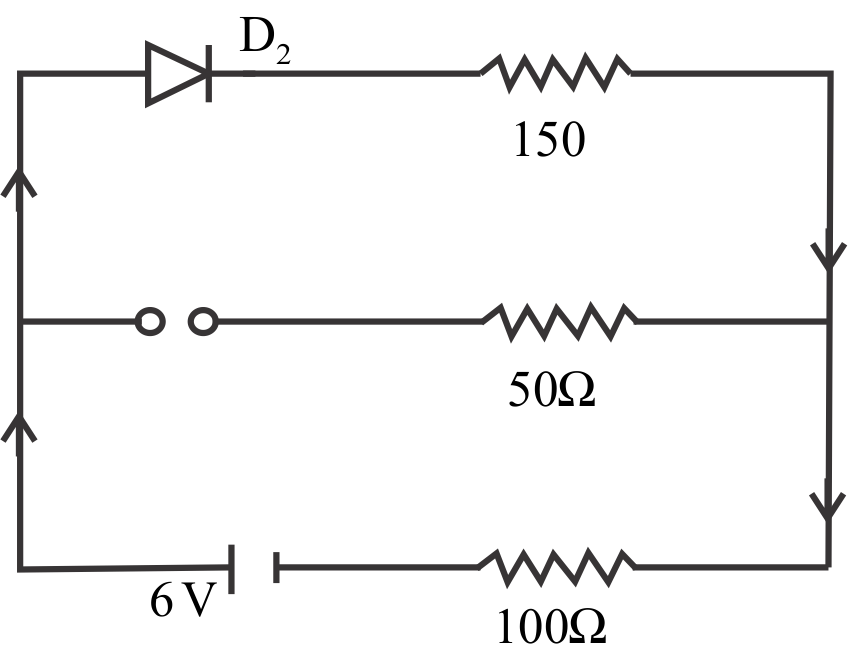
Current through 100Ω resistor is
(Given forward resistance of diode = 50Ω, reverse bias resistance = ∞ )
Solution
Hint Diode connected in forward bias conducts and that connected in reverse biased does not. We will use this concept to approach the solution. Further we will find total equivalent resistance of the circuit and find the required current.
Complete Step by step answer
Let D1 be the diode in series with 50Ω resistance and D2 be the diode in series with 150Ω resistance.
Diode D1 is reverse biased and D2 is forward biased.
Since diodes in reverse bias offer infinite resistance therefore no current flows through it. Hence all current pass-through diodes D2 .
Now we will find equivalent resistance of circuit,
Req=150Ω+100Ω+RD2
∵RD2=50Ω ∴Req=200Ω
Thus, total current in the circuit is,
I=ReqV
On putting value, we get
I=2006 I=0.03A
As all the resistances are in series, thus we get the current passing through the 100Ω resistor as 0.03A .
Note In forward biasing width of depletion layer decreases hence diode offers zero resistance and acts as a short circuit and in reverse biasing width of depletion layer increases hence it offers infinite resistance and acts as an open circuit. In open circuit no current flows in the circuit.
