If a, b, and c are in G.P., then | Mathematics - Geometric Progression (G.P.) | SolveeIt

Question

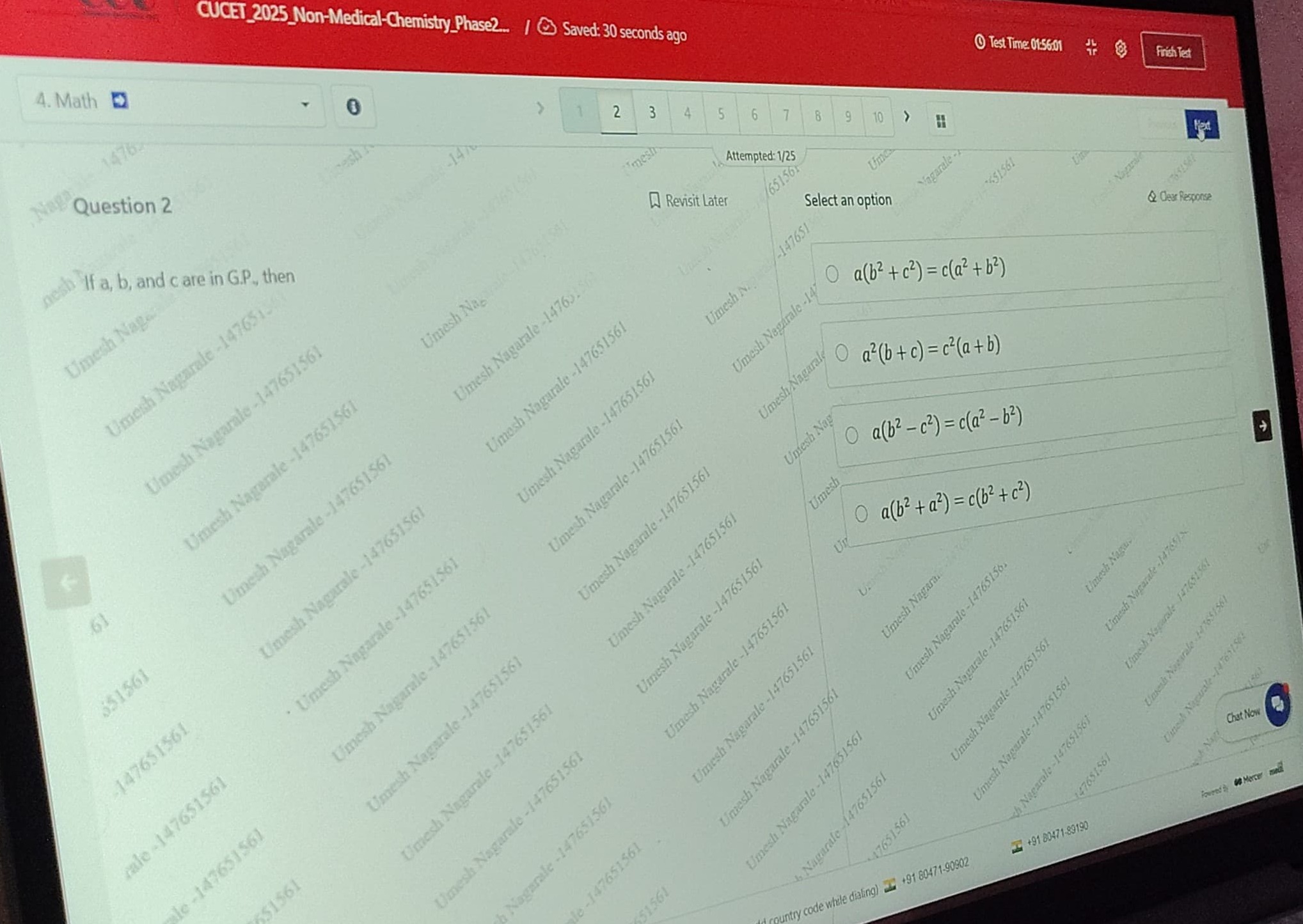
If a, b, and c are in G.P., then

$a(b^2+c^2) = c(a^2+b^2)$

$a^2(b+c) = c^2(a+b)$

$a(b^2-c^2) = c(a^2-b^2)$

$a(b^2+a^2) = c(b^2+c^2)$

Answer

$a(b^2+c^2) = c(a^2+b^2)$

Explanation

Solution

If a, b, c are in G.P., then $b^2 = ac$ . Substitute this into each option.

For option 1: $a(ac+c^2) = c(a^2+ac) \implies ac(a+c) = ac(a+c)$ , which is true.

For option 3: $a(ac-c^2) = c(a^2-ac) \implies ac(a-c) = ac(a-c)$ , which is also true.

Options 2 and 4 are not generally true. In a single-choice format, if multiple options are correct, it's a flawed question. Assuming one answer is expected, the first correct one is chosen.

Question: If a, b, and c are in G.P., then...

Solution