Question

$CsBr$ crystallizes in a body-centered cubic lattice. The unit cell length is 436.6 pm. Given that the atomic mass of $Cs = 133$ and that of $Br = 80$ amu and Avogadro number being $6.02 \times {10^{23}}mo{l^{ - 1}}$ , the density of $CsBr$ is:
A.$42.5g/c{m^3}$
B.$0.425g/c{m^3}$
C.$8.5g/c{m^3}$
D.$4.25g/c{m^3}$

Answer 1

Lattice structures are topologically ordered, three-dimensional open-celled structures composed of one or more repeating unit cells [2,3]. These cells are defined by the dimensions and connectivity of their constituent strut elements, which are connected at specific nodes.This question can be solved by using the formula $\rho = \dfrac{{Z \times M}}{{{a^3} \times {N_A}}}$ where $Z,M,a,{N_A},\rho$ are number of atoms, Mass of consisting atom/molecule, edge length/unit cell length, Avogadro number and density respectively.
Value of $Z$ for BCC is 2.

Complete step by step answer:
Let’s deduce the expression $\rho = \dfrac{{Z \times M}}{{{a^3} \times {N_A}}}$ from the very beginning.
We know density of unit cell =mass of unit cell/volume of unit cell
Mass of a unit cell = number of atoms in unit cell $\times$ mass of single atom = $Z \times m - - - (1)$ where, $Z,m$ are number of atoms and mass of single atom/molecule in unit cell. We can find the mass of a single atom/molecular by dividing atomic mass $M$ by Avogadro’s Number ${N_A}$.
So, $m = \dfrac{M}{{{N_A}}} - - - (2)$
From equation (1) & (2)
Mass of unit cell $= \dfrac{{Z \times M}}{{{N_A}}} - - - (3)$
Now we can write density of unit cell $\rho = \dfrac{{Z \times M}}{{V \times {N_A}}} - - - (4)$ where $V$ is volume of unit cell. As we also know that the volume of a cube is cube of its edge length, consider an edge length $a$ , so volume $V = {a^3}$.
So, equation (4) can be rewritten as $\rho = \dfrac{{Z \times M}}{{{a^3} \times {N_A}}} - - - (5)$ .

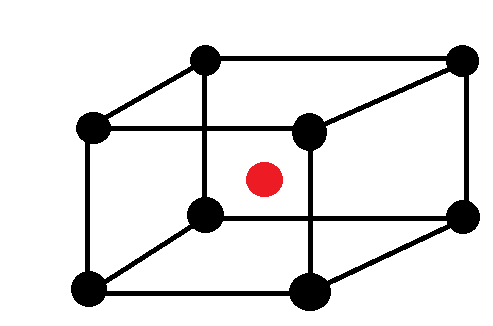
Now, Let’s calculate the number of atoms in the unit cell that is BCC.
Atoms at the corners are 8 and contribution of each corner atom is 1/8 and atom at centre is one and it is not shared with any other cell.
So, $Z = 8 \times \dfrac{1}{8} + 1 = 2$
As per question $a = 436.6pm = 436.6 \times {10^{ - 10}}cm,M = 133 + 80 = 213g/mol$
Putting all values in equation (5) we get,
$\rho = \dfrac{{2 \times 213g/mol}}{{{{(436.6 \times {{10}^{ - 10}}cm)}^3} \times 6.02 \times {{10}^{23}}mo{l^{ - 1}}}}$
$\Rightarrow \rho = 8.5g/c{m^3}$

Note:
While deducing the formula $\rho = \dfrac{{Z \times M}}{{{a^3} \times {N_A}}}$ we used $m$ and $M$ , both are different. $m$ is mass of single atom $M$ is atomic mass in amu. So, when we take $M$ atomic mass in grams, according to concept of moles, we get mass of 1 mole of atoms that are equal in Avogadro’s number $= 6.02 \times {10^{23}}mo{l^{ - 1}}$ . So, in order to find the mass of a single atom $m = \dfrac{M}{{{N_A}}}$ .