Question

A heavy particle is tied to the end A of a string of length 1.6 m. Its other end O is fixed. It revolves as a conical pendulum with the string making 60° with the vertical. Then

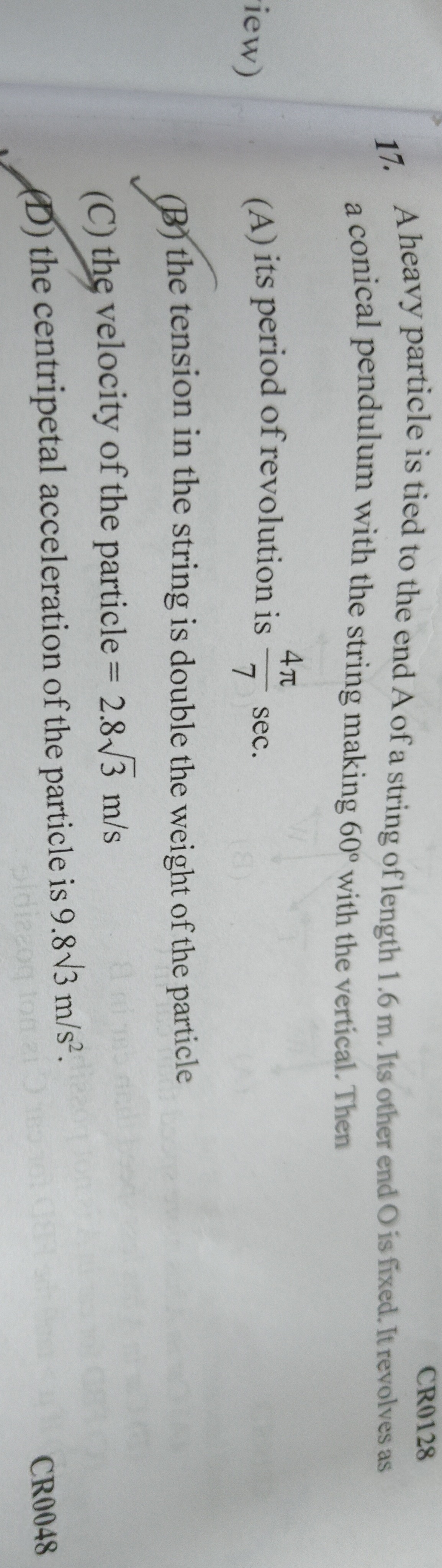
• A. its period of revolution is $\frac{4\pi}{7}$ sec.
• B. the tension in the string is double the weight of the particle
• C. the velocity of the particle = 2.8√3 m/s
• D. the centripetal acceleration of the particle is 9.8√3 m/s².

Answer 1

Answer: (A), (B), (C), (D)

All options are correct

Answer 2

The problem describes a heavy particle revolving as a conical pendulum. We need to analyze the forces and motion to determine the correctness of the given statements.

1. Setup and Forces:

Let the mass of the particle be 'm' and the length of the string be L = 1.6 m.
The string makes an angle θ = 60° with the vertical.
The forces acting on the particle are:

• Tension (T) in the string, acting along the string.
• Weight (mg) of the particle, acting vertically downwards.

2. Resolution of Forces and Equations of Motion:

Resolve the tension T into two components:

• Vertical component: T cosθ (balances the weight)
• Horizontal component: T sinθ (provides the centripetal force)

From vertical equilibrium:

$T \cos\theta = mg \quad \text{(Equation 1)}$

From horizontal motion (centripetal force):

$T \sin\theta = \frac{mv^2}{r} = m\omega^2 r \quad \text{(Equation 2)}$

where 'r' is the radius of the circular path, 'v' is the linear velocity, and 'ω' is the angular velocity.

3. Geometric Relations:

The radius of the circular path 'r' and the height 'h' of the cone are related to the string length 'L' and angle 'θ':

$r = L \sin\theta$ $h = L \cos\theta$

Given L = 1.6 m and θ = 60°:

$r = 1.6 \sin(60^\circ) = 1.6 \times \frac{\sqrt{3}}{2} = 0.8\sqrt{3} \text{ m}$ $h = 1.6 \cos(60^\circ) = 1.6 \times \frac{1}{2} = 0.8 \text{ m}$

4. Evaluate Each Option:

(B) The tension in the string is double the weight of the particle:

From Equation 1:

$T = \frac{mg}{\cos\theta}$

Substitute θ = 60°:

$T = \frac{mg}{\cos(60^\circ)} = \frac{mg}{1/2} = 2mg$

So, the tension in the string is indeed double the weight of the particle. Option (B) is correct.

(A) Its period of revolution is $\frac{4\pi}{7}$ sec:

To find the period (T_period), we can use the formula derived from the equations of motion.
Divide Equation 2 by Equation 1:

$\frac{T \sin\theta}{T \cos\theta} = \frac{m\omega^2 r}{mg}$

$\tan\theta = \frac{\omega^2 r}{g}$

Substitute $r = L \sin\theta$ and $\omega = \frac{2\pi}{T_{period}}$:

$\tan\theta = \frac{(2\pi/T_{period})^2 L \sin\theta}{g}$

$\frac{\sin\theta}{\cos\theta} = \frac{4\pi^2 L \sin\theta}{g T_{period}^2}$

$\frac{1}{\cos\theta} = \frac{4\pi^2 L}{g T_{period}^2}$

$T_{period}^2 = \frac{4\pi^2 L \cos\theta}{g}$

$T_{period} = 2\pi \sqrt{\frac{L \cos\theta}{g}}$

Substitute L = 1.6 m, θ = 60°, and g = 9.8 m/s²:

$T_{period} = 2\pi \sqrt{\frac{1.6 \times \cos(60^\circ)}{9.8}}$

$T_{period} = 2\pi \sqrt{\frac{1.6 \times (1/2)}{9.8}}$

$T_{period} = 2\pi \sqrt{\frac{0.8}{9.8}} = 2\pi \sqrt{\frac{8}{98}} = 2\pi \sqrt{\frac{4}{49}}$

$T_{period} = 2\pi \times \frac{2}{7} = \frac{4\pi}{7} \text{ sec}$ Option (A) is correct.

(C) The velocity of the particle = 2.8√3 m/s:

We can find the linear velocity 'v' using $v = \omega r$.
First, calculate angular velocity 'ω':

$\omega = \frac{2\pi}{T_{period}} = \frac{2\pi}{4\pi/7} = \frac{7}{2} \text{ rad/s}$

Now, calculate 'v':

$v = \omega r = \frac{7}{2} \times (0.8\sqrt{3})$

$v = \frac{7}{2} \times \frac{4}{5}\sqrt{3} = \frac{14}{5}\sqrt{3} = 2.8\sqrt{3} \text{ m/s}$ Option (C) is correct.

(D) The centripetal acceleration of the particle is 9.8√3 m/s²:

Centripetal acceleration $a_c = \frac{v^2}{r}$ or $a_c = \omega^2 r$.
Using $a_c = \omega^2 r$:

$a_c = \left(\frac{7}{2}\right)^2 \times (0.8\sqrt{3})$

$a_c = \frac{49}{4} \times \frac{4}{5}\sqrt{3} = \frac{49}{5}\sqrt{3} = 9.8\sqrt{3} \text{ m/s}^2$

Alternatively, from the force equations:

$T \sin\theta = m a_c$ $T \cos\theta = mg$

Dividing the first by the second:

$\tan\theta = \frac{a_c}{g}$

$a_c = g \tan\theta$

$a_c = 9.8 \tan(60^\circ) = 9.8\sqrt{3} \text{ m/s}^2$ Option (D) is correct.

All the given options (A), (B), (C), and (D) are correct statements regarding the conical pendulum described.

The final answer is $\boxed{A, B, C, D}$

Explanation of the solution:

1. Forces: Identify tension (T) and weight (mg).
2. Equilibrium/Motion Equations: Vertical equilibrium: $T \cos\theta = mg$. Horizontal centripetal force: $T \sin\theta = m\omega^2 r$.
3. Geometric Relations: Radius $r = L \sin\theta$.
4. Tension: From vertical equilibrium, $T = mg/\cos\theta = mg/\cos(60^\circ) = 2mg$. (Option B)
5. Period: Divide horizontal by vertical force equations to get $\tan\theta = \omega^2 r / g$. Substitute $\omega = 2\pi/T_{period}$ and $r = L \sin\theta$ to derive $T_{period} = 2\pi \sqrt{L \cos\theta / g}$. Calculate $T_{period} = 2\pi \sqrt{1.6 \times 0.5 / 9.8} = 4\pi/7$ sec. (Option A)
6. Velocity: Calculate angular velocity $\omega = 2\pi/T_{period} = 7/2$ rad/s. Then $v = \omega r = (7/2) \times (0.8\sqrt{3}) = 2.8\sqrt{3}$ m/s. (Option C)
7. Centripetal Acceleration: $a_c = g \tan\theta = 9.8 \tan(60^\circ) = 9.8\sqrt{3}$ m/s². (Option D)

All options are mathematically verified to be correct.