Question

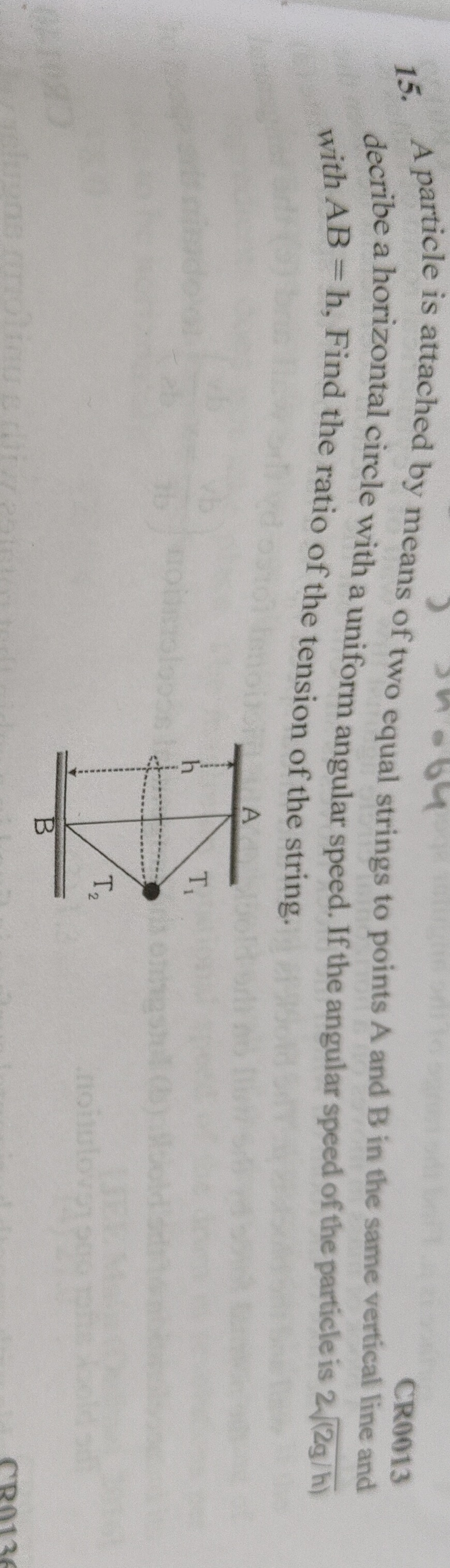
A particle is attached by means of two equal strings to points A and B in the same vertical line and decribe a horizontal circle with a uniform angular speed. If the angular speed of the particle is $2\sqrt{\frac{2g}{h}}$ with AB = h, Find the ratio of the tension of the string.

Answer 1

5:3

Answer 2

The problem describes a particle moving in a horizontal circle under the influence of two equal strings attached to points A and B in the same vertical line.

1. Diagram and Geometry:

Let the length of each string be $L$.
Let the distance between points A and B be $h$.
Since the strings are of equal length and the particle describes a horizontal circle, the horizontal plane of the circle must be exactly midway between points A and B.
Therefore, the vertical distance from A to the plane of the circle is $h/2$, and the vertical distance from B to the plane of the circle is also $h/2$.
Let $r$ be the radius of the horizontal circle.
Let $\theta$ be the angle each string makes with the vertical. From the right triangle formed by the string, the radius, and the vertical distance: $\cos \theta = \frac{h/2}{L}$
$\sin \theta = \frac{r}{L}$

2. Forces and Equations of Motion:

Let $m$ be the mass of the particle.
Let $T_1$ be the tension in the upper string (connected to A) and $T_2$ be the tension in the lower string (connected to B).
The forces acting on the particle are:

• Gravitational force: $mg$ (downwards)
• Tension $T_1$: acting along the upper string. Its vertical component is $T_1 \cos \theta$ (upwards) and its horizontal component is $T_1 \sin \theta$ (towards the center).
• Tension $T_2$: acting along the lower string. Its vertical component is $T_2 \cos \theta$ (downwards) and its horizontal component is $T_2 \sin \theta$ (towards the center).

Vertical Equilibrium:

Since the particle moves in a horizontal circle, there is no vertical acceleration. The net vertical force is zero.
$T_1 \cos \theta - T_2 \cos \theta - mg = 0$
$(T_1 - T_2) \cos \theta = mg$ --- (1)

Horizontal Motion (Centripetal Force):

The net horizontal force provides the centripetal force, $m\omega^2 r$.
$T_1 \sin \theta + T_2 \sin \theta = m\omega^2 r$
$(T_1 + T_2) \sin \theta = m\omega^2 r$ --- (2)

3. Substitute Geometric Relations:

From the geometry, we have $\cos \theta = \frac{h}{2L}$ and $\sin \theta = \frac{r}{L}$.
Substitute these into equations (1) and (2):
From (1): $(T_1 - T_2) \frac{h}{2L} = mg \implies T_1 - T_2 = \frac{2mgL}{h}$ --- (3)
From (2): $(T_1 + T_2) \frac{r}{L} = m\omega^2 r \implies T_1 + T_2 = m\omega^2 L$ --- (4)

4. Substitute Given Angular Speed:

The angular speed is given as $\omega = 2\sqrt{\frac{2g}{h}}$.
Square both sides to get $\omega^2$:
$\omega^2 = \left(2\sqrt{\frac{2g}{h}}\right)^2 = 4 \times \frac{2g}{h} = \frac{8g}{h}$

Substitute this value of $\omega^2$ into equation (4):
$T_1 + T_2 = m \left(\frac{8g}{h}\right) L = \frac{8mgL}{h}$ --- (5)

5. Solve for Tensions and Their Ratio:

Now we have a system of two linear equations for $T_1$ and $T_2$:
(3) $T_1 - T_2 = \frac{2mgL}{h}$
(5) $T_1 + T_2 = \frac{8mgL}{h}$

Add equation (3) and (5):
$(T_1 - T_2) + (T_1 + T_2) = \frac{2mgL}{h} + \frac{8mgL}{h}$
$2T_1 = \frac{10mgL}{h}$
$T_1 = \frac{5mgL}{h}$

Subtract equation (3) from (5):
$(T_1 + T_2) - (T_1 - T_2) = \frac{8mgL}{h} - \frac{2mgL}{h}$
$2T_2 = \frac{6mgL}{h}$
$T_2 = \frac{3mgL}{h}$

Finally, find the ratio of the tensions $T_1/T_2$:
$\frac{T_1}{T_2} = \frac{\frac{5mgL}{h}}{\frac{3mgL}{h}} = \frac{5}{3}$

The ratio of the tension of the string is $5:3$.

The final answer is $\boxed{5:3}$.

Explanation of the solution:

1. Identify forces: $T_1$ (upper string tension), $T_2$ (lower string tension), and $mg$ (gravity).
2. Due to equal string lengths and vertical alignment of attachment points, the particle's circular path is midway between A and B, so vertical distance from particle to A (or B) is $h/2$. Let $L$ be string length, $r$ be circle radius, $\theta$ be string angle with vertical. $\cos \theta = h/(2L)$, $\sin \theta = r/L$.
3. Apply Newton's 2nd Law:
   • Vertical equilibrium: $T_1 \cos \theta - T_2 \cos \theta - mg = 0 \implies (T_1 - T_2) \frac{h}{2L} = mg$.
   • Horizontal centripetal force: $T_1 \sin \theta + T_2 \sin \theta = m\omega^2 r \implies (T_1 + T_2) \frac{r}{L} = m\omega^2 r$.
4. Simplify equations:
   • $T_1 - T_2 = \frac{2mgL}{h}$.
   • $T_1 + T_2 = m\omega^2 L$.
5. Substitute given $\omega = 2\sqrt{\frac{2g}{h}}$ into the second simplified equation: $T_1 + T_2 = m \left(\frac{8g}{h}\right) L = \frac{8mgL}{h}$.
6. Solve the system of equations:
   • $T_1 - T_2 = \frac{2mgL}{h}$
   • $T_1 + T_2 = \frac{8mgL}{h}$
   • Adding them gives $2T_1 = \frac{10mgL}{h} \implies T_1 = \frac{5mgL}{h}$.
   • Subtracting them gives $2T_2 = \frac{6mgL}{h} \implies T_2 = \frac{3mgL}{h}$.
7. Calculate the ratio: $\frac{T_1}{T_2} = \frac{5mgL/h}{3mgL/h} = \frac{5}{3}$.