Question
Question: $\cot^2 \frac{\pi}{7} + \cot^2 \frac{2\pi}{7} + \cot^2 \frac{3\pi}{7} = 5.$...
cot27π+cot272π+cot273π=5.
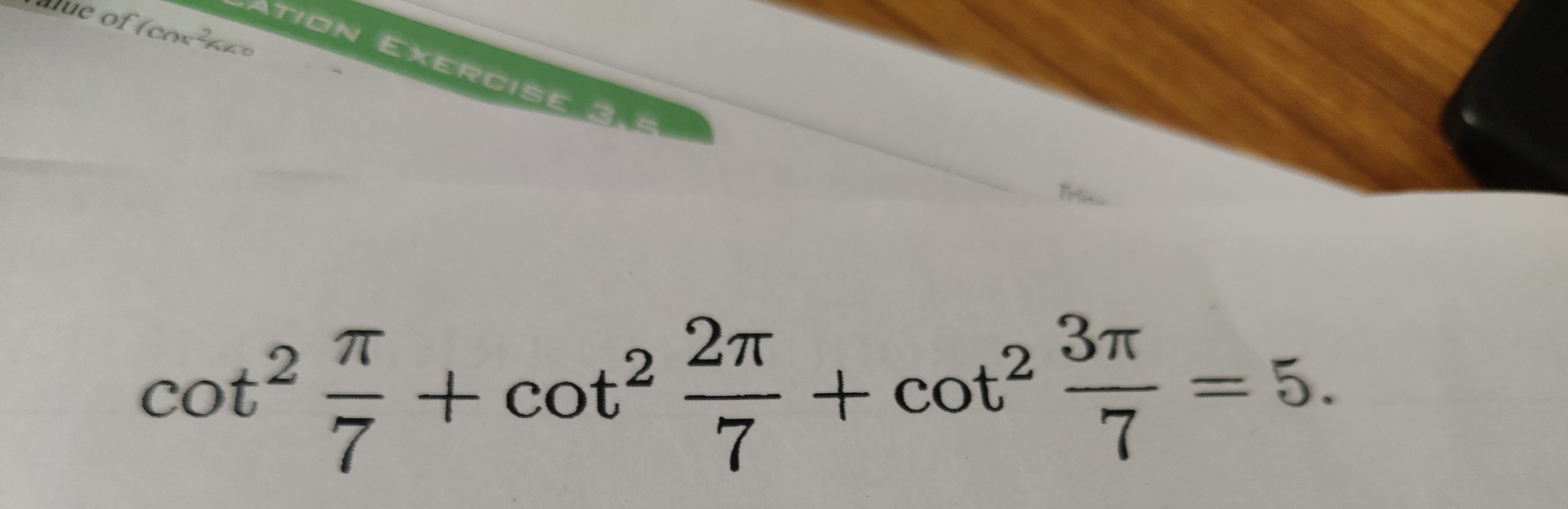
5
Solution
To verify the identity cot27π+cot272π+cot273π=5, we can use the relationship between the roots of a polynomial and trigonometric functions.
-
Consider the equation sin(7x)=0.
The solutions are x=7kπ for any integer k. We can express sin(7x) in terms of sinx and cosx using De Moivre's theorem. (cosx+isinx)7=cos(7x)+isin(7x) Expanding the left side using the binomial theorem and taking the imaginary part: sin(7x)=(17)cos6xsinx−(37)cos4xsin3x+(57)cos2xsin5x−(77)sin7x Substitute the binomial coefficients: (17)=7 (37)=3×2×17×6×5=35 (57)=(27)=2×17×6=21 (77)=1 So, the equation becomes: sin(7x)=7cos6xsinx−35cos4xsin3x+21cos2xsin5x−sin7x
-
Form a polynomial in cot2x.
For x=7kπ where k∈{1,2,3,4,5,6}, we have sin(7x)=0 and sinx=0. Divide the equation by sin7x: 0=7sin6xcos6x−35sin4xcos4x+21sin2xcos2x−1 Let y=cot2x. The equation transforms into a cubic polynomial in y: 7y3−35y2+21y−1=0
-
Identify the roots of the polynomial.
The roots of this cubic equation are the values of cot2x for x=7kπ, where k∈{1,2,3,4,5,6}. However, due to the property cot2(π−θ)=(−cotθ)2=cot2θ: cot2(74π)=cot2(π−73π)=cot2(73π) cot2(75π)=cot2(π−72π)=cot2(72π) cot2(76π)=cot2(π−7π)=cot2(7π) The angles 7π,72π,73π are distinct and lie in the first quadrant, so their cotangent values are distinct and positive. Therefore, their squares cot2(7π), cot2(72π), cot2(73π) are the three distinct roots of the cubic equation 7y3−35y2+21y−1=0.
-
Apply Vieta's formulas.
For a cubic equation ay3+by2+cy+d=0, the sum of the roots is given by −b/a. In our equation 7y3−35y2+21y−1=0: a=7, b=−35, c=21, d=−1. The sum of the roots is: cot27π+cot272π+cot273π=−7−35=735=5.
Thus, the identity is verified.
Explanation of the solution:
The identity is proven by constructing a polynomial whose roots are the terms in the sum.
- Start with the equation sin(7x)=0.
- Express sin(7x) as a polynomial in sinx and cosx using De Moivre's theorem. sin(7x)=7cos6xsinx−35cos4xsin3x+21cos2xsin5x−sin7x.
- For x=7kπ (where k=1,2,3), sin(7x)=0 and sinx=0. Divide by sin7x to get an equation in cot2x. 7cot6x−35cot4x+21cot2x−1=0.
- Let y=cot2x. This yields a cubic equation: 7y3−35y2+21y−1=0.
- The roots of this cubic equation are cot2(7π), cot2(72π), and cot2(73π). (Note: cot2(74π)=cot2(73π), etc.)
- By Vieta's formulas, the sum of the roots of ay3+by2+cy+d=0 is −b/a. Sum of roots =−(−35)/7=5.
Answer:
The given statement cot27π+cot272π+cot273π=5 is true.
