Question
Question: $\cos(\tan x) - \cos x \over x$...
xcos(tanx)−cosx
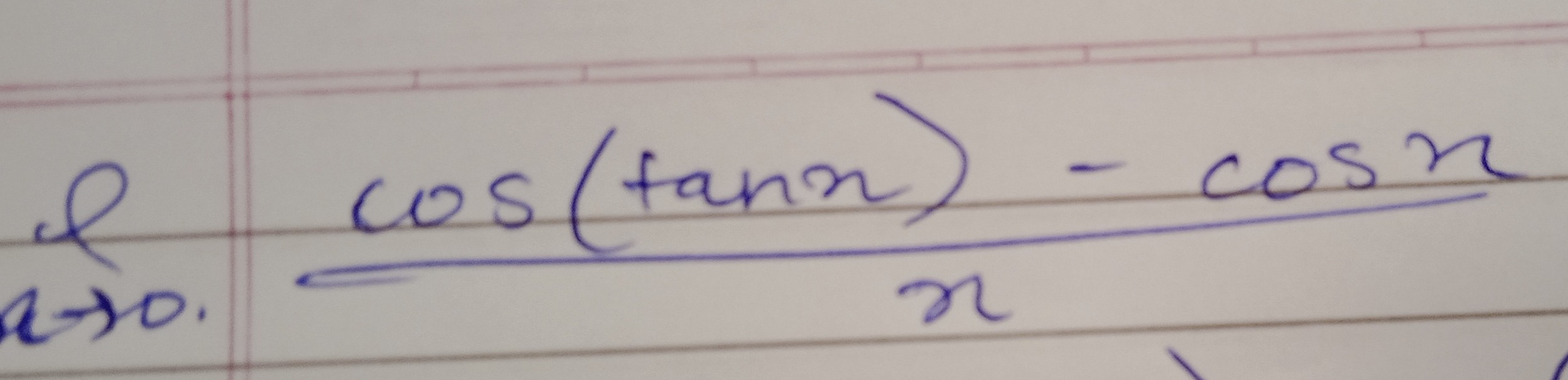
0
Solution
The problem asks to evaluate the limit of the given expression as x approaches 0: limx→0xcos(tanx)−cosx
Step 1: Check for indeterminate form. Substitute x=0 into the expression: Numerator: cos(tan0)−cos0=cos(0)−1=1−1=0. Denominator: 0. Since the limit is of the form 00, we can apply L'Hopital's Rule.
Step 2: Apply L'Hopital's Rule. L'Hopital's Rule states that if limx→ag(x)f(x) is of the form 00 or ∞∞, then limx→ag(x)f(x)=limx→ag′(x)f′(x), provided the latter limit exists.
Let f(x)=cos(tanx)−cosx and g(x)=x.
Calculate the derivative of the numerator, f′(x): f′(x)=dxd(cos(tanx)−cosx) Using the chain rule for cos(tanx): dxd(cosu)=−sinudxdu. Here u=tanx, so dxdu=sec2x. f′(x)=−sin(tanx)⋅sec2x−(−sinx) f′(x)=−sin(tanx)sec2x+sinx
Calculate the derivative of the denominator, g′(x): g′(x)=dxd(x)=1
Now, substitute these derivatives into the limit expression: limx→01−sin(tanx)sec2x+sinx
Step 3: Evaluate the limit. Substitute x=0 into the new expression: As x→0: tanx→tan0=0 sin(tanx)→sin(0)=0 secx→sec0=1, so sec2x→12=1 sinx→sin0=0
Therefore, the limit becomes: −(0)⋅(1)+0=0+0=0
The value of the limit is 0.
