Question

A point object O is placed in front of a concave mirror of focal length 20 cm. A glass slab of thickness 6 cm and of variable refractive index $\mu=\frac{1}{1-\frac{x}{9}}$, where x is the distance in cm from left surface of the slab, is introduced between the object and mirror. Consider the ray is being refracted from the slab after reflecting from mirror. The final distance of the image from the mirror is

Answer 1

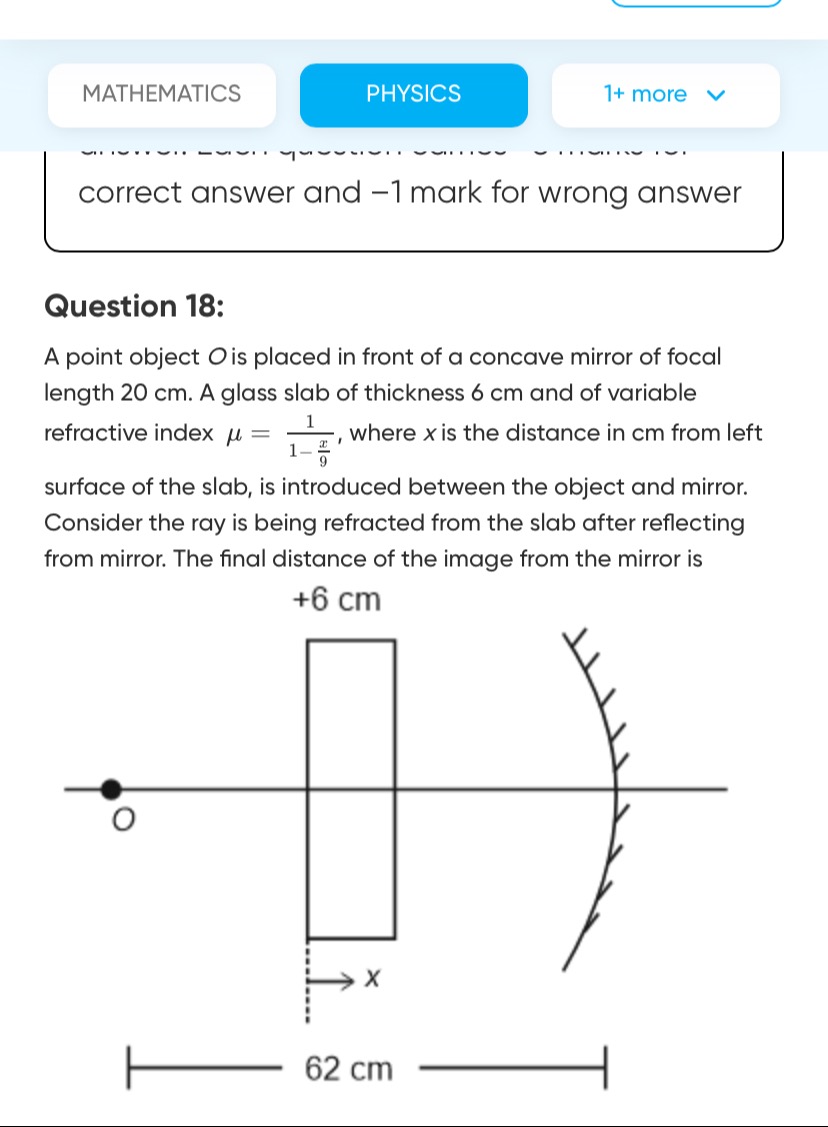
32 cm

Answer 2

The problem involves light passing through a variable refractive index slab, reflecting from a concave mirror, and then passing through the slab again.

1. Calculate the effective shift due to the slab: The refractive index of the slab is given by $\mu(x) = \frac{1}{1-\frac{x}{9}}$, where $x$ is the distance from the left surface of the slab. The thickness of the slab is $t = 6$ cm. The apparent thickness of the slab, when viewed normally, is given by: $t_{app} = \int_0^t \frac{dx}{\mu(x)}$ Substitute $\mu(x)$: $t_{app} = \int_0^6 \left(1 - \frac{x}{9}\right) dx$ $t_{app} = \left[x - \frac{x^2}{18}\right]_0^6$ $t_{app} = \left(6 - \frac{6^2}{18}\right) - (0)$ $t_{app} = 6 - \frac{36}{18} = 6 - 2 = 4$ cm

   The shift produced by the slab is $\Delta t = t - t_{app} = 6 - 4 = 2$ cm. This shift is always towards the observer.

2. First refraction (Object O to Mirror): The object O is placed at a distance of 62 cm from the concave mirror. The slab is introduced between the object and the mirror. When light from the object passes through the slab towards the mirror, the object appears closer to the mirror by the amount of shift $\Delta t$. So, the effective object distance for the mirror ($u_{eff}$) is: $u_{eff} = u_{actual} - \Delta t = 62 - 2 = 60$ cm. For the concave mirror, using sign convention (light travels from left to right, mirror is at origin, object to the left is negative): $u = -60$ cm. The focal length of the concave mirror is $f = -20$ cm.

3. Reflection from the Mirror: Using the mirror formula: $\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$ $\frac{1}{v} + \frac{1}{-60} = \frac{1}{-20}$ $\frac{1}{v} = \frac{1}{60} - \frac{1}{20}$ $\frac{1}{v} = \frac{1 - 3}{60} = \frac{-2}{60} = -\frac{1}{30}$ $v = -30$ cm. This means the image (let's call it I') formed by the mirror is real and located 30 cm in front of the mirror (to the left of the mirror).

4. Second refraction (Image I' to Final Image I''): The light rays, after reflecting from the mirror, travel back through the slab towards the observer (implicitly on the left side, where the original object was). The image I' acts as an object for this second refraction through the slab. The image I' is formed at 30 cm from the mirror. Since the slab is between the object and the mirror, the light rays from I' must pass through the slab to reach the observer. The shift due to the slab is $\Delta t = 2$ cm, and it is always towards the observer. Since I' is formed 30 cm to the left of the mirror, and the observer is also to the left, the final image I'' will be shifted further to the left (towards the observer). Therefore, the final distance of the image from the mirror will be: $d_{final} = |v| + \Delta t = 30 + 2 = 32$ cm.