Question

Convert the given frequency distribution into a continuous grouped frequency distribution:

In which intervals would $153.5$ and $157.5$ be included?
A) $153.5 - 157.5$ and $161.5 - 165.5$
B) $153.5 - 157.5$ and $149.5 - 153.5$
C) $153.5 - 157.5$ and $157.5 - 161.5$
D) $153.5 - 157.5$ and $149.5 - 153.5$

Answer 1

The given frequencies are not in continuous intervals. It implies that the midpoints of a starting point and end point are not included in class. Thus, first we will convert the given class intervals into the continuous group frequency so that each and every point is included in the classes.

Complete step-by-step answer:
Observe that the given table has discontinued frequency distribution so first we will convert it into continuous frequency distribution.
Consider the upper limit of the first class and lower limit of the next class.
The upper limit of the class $150 - 153$ is $153$ .
The lower limit of the class $154 - 157$ is $154$ .
We will find the midpoint of the above two points.
$\dfrac{{154 - 153}}{2} = 0.5$
We will add this number to each upper limit and subtract the same number from the lower limit of each class.
We will illustrate the first example.
The lower limit of the first class $150 - 153$ is $150$.
Thus, it will get converted to $150 - 0.5 = 149.5$ .
Similarly, the upper limit of the class $150 - 153$ is $153$ .
Thus, it will get converted to $153 + 0.5 = 153.5$ .
Therefore, the first class becomes $149.5 - 153.5$ .
We will use the similar technique and convert the given table as follows:

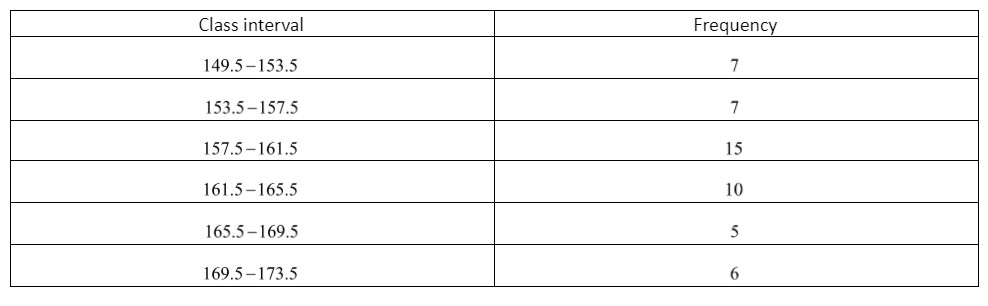
Now observe that each number is included now.
Thus, we observe that $153.5$ is included in the class $153.5 - 157.5$ and $157.5$ is included in the class $157.5 - 161.5$.

So, the correct answer is “Option C”.

Note: Here we find the midpoint of each class so that every point will be included in the class intervals. Next important point is we include a lower limit in each of the corresponding class. We include the upper class of each of the continuous class in the next class.