Question

Construct the circumcircle and incircle of an equilateral $\Delta ABC$ with side 6cm and center $O$. Find the ratio of radii of circumcircle and incircle.

Answer 1

Hint: Draw a perpendicular bisector on the equilateral triangle which divides the sides of the equilateral triangle into two equal parts. Take their intersection point to draw a circumcircle and incircle. Now use trigonometric ratios in two different triangles for values of in-radius and circum-radius.

Complete step-by-step answer:

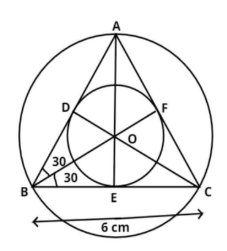
The pictorial representation of the given problem is shown above.
The equilateral triangle ABC with side 6 cm has a circumcircle and an incircle with center O and radii ${r_1}$ and ${r_2}$ respectively.
$\Rightarrow OB = {r_1}cm,{\text{ }}OD = {r_2}cm$
AE and CD are the perpendicular bisector of BC and AB respectively.
$\Rightarrow BE = CE = BD = AD = \dfrac{6}{2} = 3cm$
Since, FB is the bisector of $\angle ABC$
$\Rightarrow \angle FBC = \angle FBA = \dfrac{{{{60}^0}}}{2} = {30^0}$
Because in equilateral triangle all angles are equal which is ${60^0}$
Now, in $\Delta OBE,{\text{ cos3}}{{\text{0}}^0}{\text{ = }}\dfrac{{BE}}{{OB}} = \dfrac{3}{{{r_1}}}$
As we know ${\text{cos3}}{{\text{0}}^0} = \dfrac{{\sqrt 3 }}{2}$
$\Rightarrow {r_1} = \dfrac{3}{{\cos {{30}^0}}} = \dfrac{3}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{6}{{\sqrt 3 }}cm$
Now in $\Delta OBD,{\text{ tan3}}{{\text{0}}^0}{\text{ = }}\dfrac{{OD}}{{BD}} = \dfrac{{{r_2}}}{3}$
As we know ${\text{tan3}}{{\text{0}}^0} = \dfrac{1}{{\sqrt 3 }}$
$\Rightarrow {r_2} = 3\tan {30^0} = 3\left( {\dfrac{1}{{\sqrt 3 }}} \right) = \sqrt 3 cm$
Now you have to calculate the ratio of radii circumcircle to incircle
$\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{{\dfrac{6}{{\sqrt 3 }}}}{{\sqrt 3 }} = \dfrac{6}{{\sqrt 3 \times \sqrt 3 }} = \dfrac{6}{3} = 2cm$
So, the required ratio of the radii is 2 cm.

Note: In such types of question first draw the pictorial representation of the given problem, then draw the perpendicular bisectors on the triangle which divide its sides into two equal parts, then apply basic trigonometric property and calculate the radii of the two circles, then divide them we will get the required answer.