Question

Construct a triangle PQR in which $\angle {\rm{Q = 30}}^\circ$, $\angle R = 90^\circ$ and ${\rm{PQ}} + {\rm{QR}} + {\rm{PR}} = {\rm{11}}\,{\rm{cm}}$.

Answer 1

Here, to construct this triangle use the method of construction of a right angle triangle whose two angles were given with the sum of all three sides.

Complete Step-by-step Solution
Given,
The angle Q is $\angle {\rm{Q = 30}}^\circ$.
The angle R is $\angle R = 90^\circ$.
The sum of lines are ${\rm{PQ}} + {\rm{QR}} + {\rm{PR}} = {\rm{11}}\,{\rm{cm}}$.

The following are the steps to construct a triangle PQR.

1. Draw the base line AB equal to ${\rm{PQ}} + {\rm{QR}} + {\rm{PR}} = {\rm{11}}\,{\rm{cm}}$.

2. Now draw an angle of $30^\circ$ from point A and $90^\circ$ from point B.

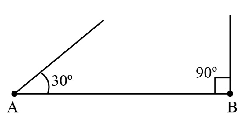
3. Bisects these angles and extend the bisector to intersect with each other, mark the intersection point of the bisector of angles as P.

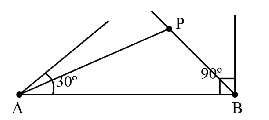
4. Now draw a perpendicular bisector of line AP and BP. Name the bisector of AB as DE and bisector of BP as FG.

6. Extend the perpendicular bisectors DE and FG to cut the base line. DE cuts AB at point Q and FG cuts AB at point R.

7. Join PQ and PR. Now $\Delta PQR$ is required triangle.

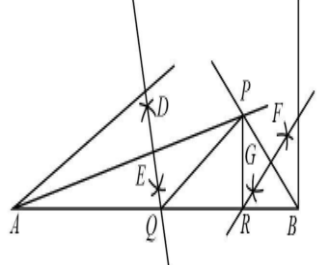
Therefore, $\Delta PQR$ is a required triangle that we construct.

Note: In such types of problems, while making bisectors of angles remember that radius of compass should be the same to bisect an angle and use a sharp pencil to draw points and to get accurate results.