Question

Considering Ellingham Diagram, which of the following metals can be used to reduce alumina?
A.Mg
B.Fe
C.Cu
D.Zn

Answer 1

For this question we have to look into the Ellingham diagram. The element whose line will lie below the line for formation of alumina in the Ellingham diagram will be used for reduction. Alumina is aluminum oxide.

Complete step by step answer:
Ellingham diagram is a graph between $\Delta {\text{G}}^\circ$ that is standard Gibbs free energy and temperature in Kelvin. All the curves in the Ellingham diagram represent the formation of oxides of a metal.
The Ellingham diagram is as follow:

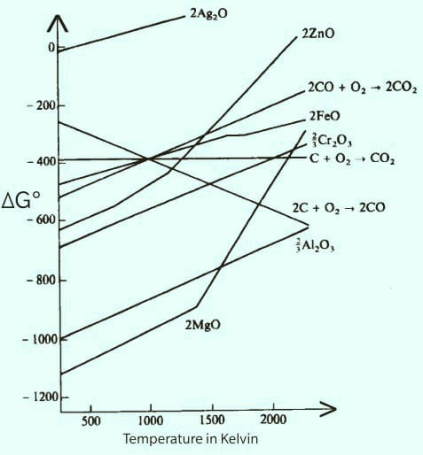
$\Delta {\text{G}}^\circ$ tells us about the spontaneity of a reaction. Positive value of $\Delta {\text{G}}^\circ$ means the reaction is feasible or spontaneous and the negative value of $\Delta {\text{G}}^\circ$ makes the reaction non spontaneous. More is the negative value of $\Delta {\text{G}}^\circ$ greater is the feasibility or tendency of reaction to form products. So if in the Ellingham diagram the formation of alumina is occurring at $\Delta {\text{G}}^\circ$ equals -1000. And the formation of magnesium oxide line lies below it and has more $\Delta {\text{G}}^\circ$ value in negative. Hence magnesium has more tendencies to form oxide than aluminium. So if we react magnesium with alumina, magnesium has more tendency to get oxidized and hence will reduce another one that is alumina.
All the other metal lies above aluminium and hence less tendency to oxidize so cannot reduce alumina.

Hence the correct option is A.

Note:
In the Ellingham diagram the entropy slope of all the lines is generally positive. This is because gases are forming solid oxides, which is why the degree of randomness decreases and $\Delta {\text{S}}$ will have negative value. We know $\Delta {\text{G}}^\circ = \Delta {\text{H}} - {\text{T}}\Delta {\text{S}}$ and the graph between $\Delta {\text{G}}^\circ$ and T will yield slope equals to $- \Delta {\text{S}}$ according to linear straight line equation. The value of $\Delta {\text{S}}$ is negative that makes the overall slope positive.