Question

Consider two straight lines, each of which is tangent to both the circle ${{x}^{2}}+{{y}^{2}}=\dfrac{1}{2}$ and the parabola ${{y}^{2}}=4x$. Let these lines intersect at the point Q. Consider the ellipse whose centre is at the origin $O\left( 0,0 \right)$ and whose semi – major axis is OQ. If the length of the minor axis of this ellipse is $\sqrt{2}$, then which of the following statement(s) is (are) true?
(a)For the ellipse, the eccentricity is $\dfrac{1}{\sqrt{2}}$ and the length of the latus rectum is 1.
(b) For the ellipse, the eccentricity is $\dfrac{1}{2}$ and the length of the latus rectum is $\dfrac{1}{2}$.
(c) The area of the region bounded by the ellipse between the lines $x=\dfrac{1}{\sqrt{2}}\And x=1$ is $\dfrac{1}{4\sqrt{2}}\left( \pi -2 \right)$
(d) The area of the region bounded by the ellipse between the lines $x=\dfrac{1}{\sqrt{2}}\And x=1$ is $\dfrac{1}{16\sqrt{2}}\left( \pi -2 \right)$

Answer 1

We know that, the equation of tangent of the parabola ${{y}^{2}}=4ax$ with slope m is equal to $y=mx+\dfrac{a}{m}$. So, using this relation we can find the equation of tangent to the parabola ${{y}^{2}}=4x$. The circle is also touching that tangent so write the length of the perpendicular from the centre of the circle to the tangent and then equate it to the radius of the circle. Now, from this equation we will get the value of m. After that substitute these values of m in the tangent equation will give you the equation of tangents. The intersection of these tangents will give you the coordinates of point Q. Now, to write the equation of the ellipse we need the length of the semi- (major and minor) axis. Length of minor axis is given and length of semi major axis is OQ. We know the coordinates of O and Q so using the distance formula we can find the length of OQ. From the equation of the ellipse, we can find eccentricity and the latus rectum.

Complete step-by-step answer:
In the below figure, we have drawn two tangents which are touching both the circle ${{x}^{2}}+{{y}^{2}}=\dfrac{1}{2}$ and the parabola ${{y}^{2}}=4x$.

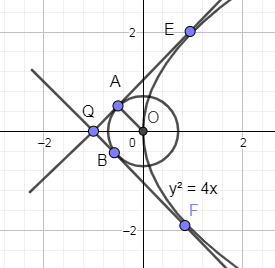
In the above figure, you can see that QE and QF are the common tangents of the circle and the parabola and the two tangents intersect each other at point Q.
Now, we know that equation of the tangent to the parabola ${{y}^{2}}=4ax$ with slope m is equal to:
$y=mx+\dfrac{a}{m}$………… Eq. (1)
The parabola given in this problem is equal to:
${{y}^{2}}=4x$……… Eq. (2)
On comparing the above parabola to ${{y}^{2}}=4ax$ we get the value of “a” as 1 so substituting the value of “a” as 1 in eq. (1) we get,
$y=mx+\dfrac{1}{m}$………. Eq. (3)
We can write the above equation in the form of $ax+by+c=0$ as follows:
$mx-y+\dfrac{1}{m}=0$
Now, this equation is tangent to circle of the equation ${{x}^{2}}+{{y}^{2}}=\dfrac{1}{2}$ so length of the perpendicular from the centre of the circle O (0, 0) to the tangent is equal to the radius of the circle.
Now, we know that if a line $ax+by+c=0$ is given then length of the perpendicular to this line from the point $Z\left( {{x}_{1}},{{y}_{1}} \right)$ is equal to:
$\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
Using the above relation, we can find the length of the perpendicular from the centre of the circle O(0, 0) to the tangent.
$\dfrac{\left| m\left( 0 \right)-\left( 0 \right)+\dfrac{1}{m} \right|}{\sqrt{{{m}^{2}}+1}}$
Now, we have given the equation of a circle as:
${{x}^{2}}+{{y}^{2}}=\dfrac{1}{2}$
In the above equation, $\dfrac{1}{2}$ is the square of the radius of the circle so the radius of the circle is the square root of $\dfrac{1}{2}$. Hence, the radius of the circle is equal to:
$\dfrac{1}{\sqrt{2}}$
Now, equating the above radius to length of the perpendicular we get,
$\begin{aligned} & \dfrac{\left| m\left( 0 \right)-\left( 0 \right)+\dfrac{1}{m} \right|}{\sqrt{{{m}^{2}}+1}}=\dfrac{1}{\sqrt{2}} \\\ & \Rightarrow \dfrac{1}{m\left( \sqrt{{{m}^{2}}+1} \right)}=\dfrac{1}{\sqrt{2}} \\\ \end{aligned}$
Cross multiplying of the above equation we get,
$\sqrt{2}=m\sqrt{{{m}^{2}}+1}$
Squaring both the sides of the above equation we get,
$\begin{aligned} & 2={{m}^{2}}\left( {{m}^{2}}+1 \right) \\\ & \Rightarrow {{m}^{4}}+{{m}^{2}}-2=0 \\\ \end{aligned}$
In the above equation, we can write ${{m}^{2}}$ as $2{{m}^{2}}-{{m}^{2}}$.

& {{m}^{4}}+2{{m}^{2}}-{{m}^{2}}-2=0 \\\ & \Rightarrow {{m}^{2}}\left( {{m}^{2}}+2 \right)-1\left( {{m}^{2}}+2 \right)=0 \\\ \end{aligned}$$ Taking ${{m}^{2}}+2$ as common from the above equation we get, $\left( {{m}^{2}}+2 \right)\left( {{m}^{2}}-1 \right)=0$ Solving above equation by equating $\left( {{m}^{2}}+2 \right)\And \left( {{m}^{2}}-1 \right)$ to 0 we get, $\begin{aligned} & {{m}^{2}}+2=0 \\\ & \Rightarrow {{m}^{2}}=-2 \\\ \end{aligned}$ Square of any term cannot be negative so the above equation has imaginary roots. $\begin{aligned} & {{m}^{2}}-1=0 \\\ & \Rightarrow \left( m+1 \right)\left( m-1 \right)=0 \\\ & \Rightarrow m=\pm 1 \\\ \end{aligned}$ Substituting the above values of m in eq. (3) we get, $\begin{aligned} & y=\left( 1 \right)x+\dfrac{1}{1} \\\ & \Rightarrow y=x+1 \\\ & y=\left( -1 \right)x+\dfrac{1}{\left( -1 \right)} \\\ & \Rightarrow y=-\left( x+1 \right) \\\ \end{aligned}$ Hence, we have got the equations of tangent to circle and parabola as: $\begin{aligned} & y=x+1......Eq.(4) \\\ & y=-\left( x+1 \right)..........Eq.(5) \\\ \end{aligned}$ Now, intersection of both these tangents is point Q so finding the intersection point of the above equations by adding eq. (4) and eq.(5) we get, $\begin{aligned} & 2y=0 \\\ & \Rightarrow y=0 \\\ \end{aligned}$ Substituting the above value of y in eq. (4) we get, $\begin{aligned} & 0=x+1 \\\ & \Rightarrow x=-1 \\\ \end{aligned}$ Hence, we have got the coordinates of point Q as (-1, 0). Now, we are going to find the equation of an ellipse whose length of minor axis is given as $\sqrt{2}$ and length of semi major axis is given as OQ. We know the coordinates of O and Q as follows: $O\left( 0,0 \right)\And Q\left( -1,0 \right)$ The distance between these points is calculated as follows: $\begin{aligned} & \sqrt{{{\left( -1-0 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}} \\\ & =1 \\\ \end{aligned}$ Hence, we have got the length of semi major axis as 1 and length of semi minor axis is the half of $\sqrt{2}$ $\left( i.e.\dfrac{\sqrt{2}}{2} \right)$. The equation of the ellipse that we have to find has a centre at origin. We know that equation of an ellipse with centre at origin (0, 0) is equal to: $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ Now, substituting $a=1$ and $b=\dfrac{\sqrt{2}}{2}=\dfrac{1}{\sqrt{2}}$ in the above equation we get, $\dfrac{{{x}^{2}}}{\left( 1 \right)}+\dfrac{{{y}^{2}}}{\left( \dfrac{1}{2} \right)}=1$ We have to find the eccentricity and latus rectum of this ellipse and we know that, The eccentricity of the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is given as: $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ Substituting ${{a}^{2}}=1,{{b}^{2}}=\dfrac{1}{2}$ in the above equation we get, $\begin{aligned} & e=\sqrt{1-\dfrac{1}{2}} \\\ & \Rightarrow e=\sqrt{\dfrac{2-1}{2}}=\dfrac{1}{\sqrt{2}} \\\ \end{aligned}$ The length of latus rectum of the ellipse is given as: $\dfrac{2{{b}^{2}}}{a}$ Substituting the value of a and b from the above we get, $\begin{aligned} & \dfrac{2{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}}{1} \\\ & =2\left( \dfrac{1}{2} \right) \\\ & =1 \\\ \end{aligned}$ Hence, we have got the eccentricity as $\dfrac{1}{\sqrt{2}}$ and latus rectum as 1. Now, we are going to find the area of the region bounded by the ellipse $\dfrac{{{x}^{2}}}{\left( 1 \right)}+\dfrac{{{y}^{2}}}{\left( \dfrac{1}{2} \right)}=1$ and the lines $x=\dfrac{1}{\sqrt{2}}\And x=1$ so we are going to integrate the y from the ellipse in the limits of $x=\dfrac{1}{\sqrt{2}}tox=1$. $\int\limits_{\dfrac{1}{\sqrt{2}}}^{1}{ydx}$ Now, writing “y” in terms of x from the equation of an ellipse we get, $\begin{aligned} & \dfrac{{{x}^{2}}}{\left( 1 \right)}+\dfrac{{{y}^{2}}}{\left( \dfrac{1}{2} \right)}=1 \\\ & \Rightarrow 2{{y}^{2}}=1-{{x}^{2}} \\\ & \Rightarrow y=\pm \sqrt{\dfrac{1-{{x}^{2}}}{2}} \\\ \end{aligned}$ We are substituting the positive value of y in $\int\limits_{\dfrac{1}{\sqrt{2}}}^{1}{ydx}$ we get, $\int\limits_{\dfrac{1}{\sqrt{2}}}^{1}{\sqrt{\dfrac{1-{{x}^{2}}}{2}}dx}$ Let us assume x as $\sin \theta $ we get, $x=\sin \theta $ Differentiating on both the sides we get, $dx=\cos \theta d\theta $ Then the above limits also got changed as follows: The lower limit when x equals: $x=\dfrac{1}{\sqrt{2}}$ Writing x as $\sin \theta $ we get, $\sin \theta =\dfrac{1}{\sqrt{2}}$ The above value holds true when $\theta =\dfrac{\pi }{4}$ so the lower limit in $\theta $ is equal to $\dfrac{\pi }{4}$. The upper limit in $\theta $ is equal to: $\begin{aligned} & x=1 \\\ & \Rightarrow \sin \theta =1 \\\ & \Rightarrow \theta =\dfrac{\pi }{2} \\\ \end{aligned}$ Now, substituting the limits in the integration and all the places where there are “x” in terms of $\theta $ we get, $$\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\sqrt{\dfrac{1-{{\sin }^{2}}\theta }{2}}\cos \theta d\theta }$$ We know that, $1-{{\sin }^{2}}\theta ={{\cos }^{2}}\theta $ so using this relation in the above integration we get, $$\begin{aligned} & \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\sqrt{\dfrac{{{\cos }^{2}}\theta }{2}}\cos \theta d\theta } \\\ & \Rightarrow \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\dfrac{1}{\sqrt{2}}\cos \theta \cos \theta d\theta } \\\ & =\dfrac{1}{\sqrt{2}}\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{{{\cos }^{2}}\theta d\theta } \\\ \end{aligned}$$ We that, ${{\cos }^{2}}\theta =\dfrac{1+\cos 2\theta }{2}$ so using this relation in the above integral we get, $$\begin{aligned} & \dfrac{1}{\sqrt{2}}\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\left( \dfrac{1+\cos 2\theta }{2} \right)d\theta } \\\ & =\dfrac{1}{2\sqrt{2}}\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\left( 1+\cos 2\theta \right)d\theta } \\\ \end{aligned}$$ Writing the integration of the expression written in the bracket we get, $\dfrac{1}{2\sqrt{2}}\left| \theta +\dfrac{\sin 2\theta }{2} \right|_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}$ Applying the lower and upper limit we get, $\dfrac{1}{2\sqrt{2}}\left| \dfrac{\pi }{2}+\dfrac{\sin \dfrac{2\pi }{2}}{2}-\left( \dfrac{\pi }{4}+\dfrac{\sin \dfrac{2\pi }{4}}{2} \right) \right|$ $=\dfrac{1}{2\sqrt{2}}\left| \dfrac{\pi }{2}-\dfrac{\pi }{4}+\dfrac{\sin \pi }{2}-\dfrac{\sin \dfrac{\pi }{2}}{2} \right|$ $=\dfrac{1}{2\sqrt{2}}\left| \dfrac{2\pi -\pi }{4}+\dfrac{\sin \pi }{2}-\dfrac{\sin \dfrac{\pi }{2}}{2} \right|$ We know that, $\sin \pi =0,\sin \dfrac{\pi }{2}=1$ so using these values in the above relation we get, $\begin{aligned} & \dfrac{1}{2\sqrt{2}}\left| \dfrac{\pi }{4}+0-\dfrac{1}{2} \right| \\\ & =\dfrac{1}{2\sqrt{2}}\left| \dfrac{\pi }{4}-\dfrac{1}{2} \right| \\\ \end{aligned}$ Hence, we got the area under the curve positive value of y in the ellipse is: $\dfrac{1}{2\sqrt{2}}\left( \dfrac{\pi }{4}-\dfrac{1}{2} \right)$ By symmetry, the negative value of y of the ellipse also gets the same value so the final answer is the multiplication of the above area by 2. $\begin{aligned} & \dfrac{1}{2\sqrt{2}}\left( \dfrac{\pi }{4}-\dfrac{1}{2} \right)2 \\\ & =\dfrac{1}{\sqrt{2}}\left( \dfrac{\pi }{4}-\dfrac{1}{2} \right) \\\ \end{aligned}$ Hence, we got the area of the region bounded by the ellipse $\dfrac{{{x}^{2}}}{\left( 1 \right)}+\dfrac{{{y}^{2}}}{\left( \dfrac{1}{2} \right)}=1$ and the lines $x=\dfrac{1}{\sqrt{2}}\And x=1$ is equal to $\dfrac{1}{\sqrt{2}}\left( \dfrac{\pi }{4}-\dfrac{1}{2} \right)$. **So, the correct answer is “Option A and C”.** **Note:** The mistake that you could make in this problem is in writing the value of semi major and semi minor axis in place of a and b in the equation of an ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. You might have put the length of major or minor axis in place of “a and b” which is wrong because “a and b” in the equation of an ellipse is the length of semi major or minor axis. Generally, this mistake is seen so make sure you won’t make this mistake.