Question

Consider two fixed points $A(1, 0, 0)$ and $P(1, 0, 1)$. If $OA$ (where '$O$' is origin) is rotated through '$O$' in $xy$-plane by a variable angle $\theta$, to reach a new position $OB$, then which of the following statement(s) is (are) correct?

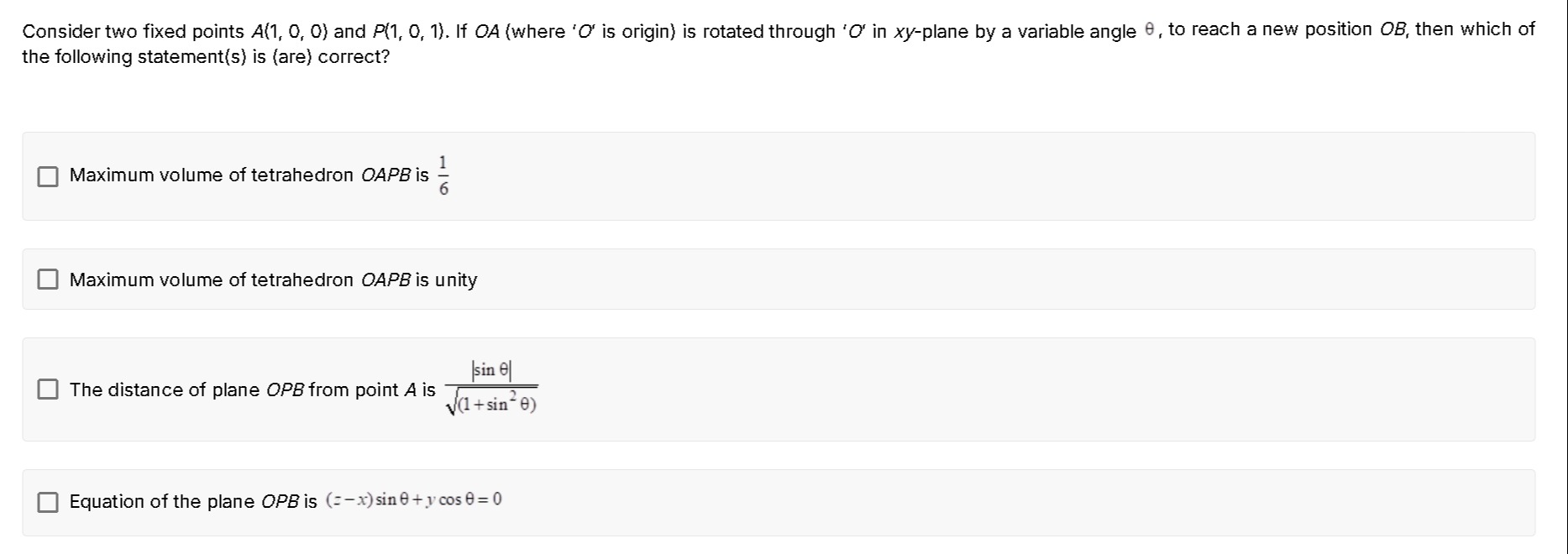
• A. Maximum volume of tetrahedron $OAPB$ is $\frac{1}{6}$
• B. Maximum volume of tetrahedron $OAPB$ is unity
• C. The distance of plane $OPB$ from point $A$ is $\frac{|\sin\theta|}{\sqrt{(1+\sin^2\theta)}}$
• D. Equation of the plane $OPB$ is $(-x)\sin\theta + y\cos\theta = 0$

Answer 1

Answer: (A), (C)

Options 1 and 3 are correct.

Answer 2

1. Coordinates:

• $O = (0,0,0)$
• $A = (1,0,0)$
• $P = (1,0,1)$
• $B$ is the image of $A$ rotated in the $xy$–plane by $\theta$: $$B=(\cos\theta,\sin\theta,0)$$

2. Volume of Tetrahedron $OAPB$:

The volume is given by:

$$V=\frac{1}{6}\left| \det\begin{pmatrix} 1 & 1 & \cos\theta\\[1mm] 0 & 0 & \sin\theta\\[1mm] 0 & 1 & 0 \end{pmatrix}\right|$$

Calculating the determinant:

$$\det = 1\bigl(0\cdot0-\sin\theta\cdot1\bigr) - 1\bigl(0\cdot0-\sin\theta\cdot0\bigr) + \cos\theta\bigl(0\cdot1-0\cdot0\bigr) = -\sin\theta.$$

Thus,

$$V = \frac{1}{6}|\sin\theta|.$$

The maximum occurs when $|\sin\theta|=1$, so maximum $V=\frac{1}{6}$.

3. Distance of Point $A$ from Plane $OPB$:

Find the plane containing $O$, $P$ and $B$.

• Vectors in the plane: $$\vec{OP}=(1,0,1), \quad \vec{OB}=(\cos\theta,\sin\theta,0)$$
• Normal vector $\vec{n}=\vec{OP}\times\vec{OB}$: $$\vec{n}= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\[2mm] 1 & 0 & 1\\[2mm] \cos\theta & \sin\theta & 0 \end{vmatrix} =\bigl(-\sin\theta,\cos\theta,\sin\theta\bigr).$$
• Equation of the plane (through $O$) is: $$-\sin\theta\,x +\cos\theta\,y+\sin\theta\,z=0.$$
• Distance from $A=(1,0,0)$ to the plane is: $$d=\frac{| \vec{n}\cdot A |}{\|\vec{n}\|} =\frac{|- \sin\theta\cdot1 + \cos\theta\cdot0+\sin\theta\cdot0|}{\sqrt{(\sin\theta)^2+(\cos\theta)^2+(\sin\theta)^2}} =\frac{|\sin\theta|}{\sqrt{1+ \sin^2\theta}}.$$

4. Verification of Statements:

• Statement 1: "Maximum volume of tetrahedron $OAPB$ is $\frac{1}{6}$".
  $\checkmark$ True.
• Statement 2: "Maximum volume of tetrahedron $OAPB$ is unity".
  False.
• Statement 3: "The distance of plane $OPB$ from point $A$ is $\frac{|\sin\theta|}{\sqrt{(1+\sin^2\theta)}}$".
  $\checkmark$ True.
• Statement 4: "Equation of the plane $OPB$ is $(-x)\sin\theta + y\cos\theta = 0$".
  The correct equation (from above) is $$-\sin\theta\,x+\cos\theta\,y+\sin\theta\,z=0.$$ Lacking the $z$-term, this statement is False.