Question
Question: Consider triangle ABC, right angled at C in which AB = 29 units, BC = 21 units and \(\angle ABC=\the...
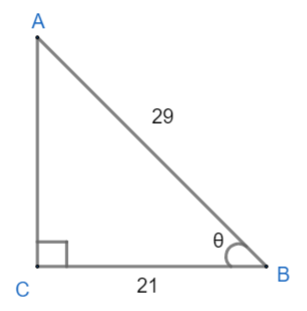
Consider triangle ABC, right angled at C in which AB = 29 units, BC = 21 units and ∠ABC=θ (see fig.) Determine the value of cos2θ+sin2θ.
Solution
In this question, we are given a right angled triangle along with measurements of base and hypotenuse of the triangle. We need to find the value of cos2θ+sin2θ. For this, we will first find the value of the perpendicular of the right angled triangle, using Pythagoras theorem. Pythagora's theorem states that, the sum of the squares of the perpendicular and the base of the triangle is equal to the square of the hypotenuse. After that, we will find the value of cosθ and sinθ and use them to find the value of cos2θ+sin2θ.
We will use cosθ=HypotenuseSide adjacent to angle θ=HypotenuseBase and
sinθ=HypotenuseSide opposite to angle θ=HypotenusePerpendicular.
Complete step-by-step answer:
Here we are given ΔABC with AB = 29 and BC = 21. Since, ΔABC=θ so according to the diagram, base = 21 and hypotenuse = 29.
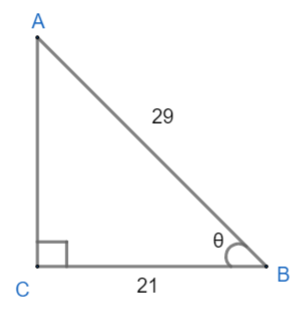
Now, let us first find the value of AC using Pythagoras theorem.
According to the Pythagoras theorem, the sum of the squares of the perpendicular and the base of the triangle is equal to the square of the hypotenuse. Hence,
(Hypotenuse)2=(Perpendicular)2+(Base)2
According to the diagram,
