Question
Question: Consider the YDSE arrangement shown in the figure. If d = 10\(\lambda \) and the position of the 8th...
Consider the YDSE arrangement shown in the figure. If d = 10λ and the position of the 8th maxima is (3xD) then find the value of x.
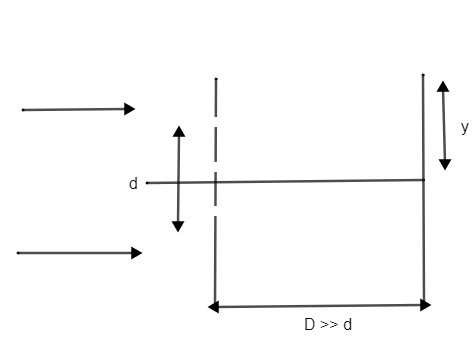
Solution
In order to solve this question we will use a formula for the 8th maxima using the young’ double slit formula and by putting required values in the formula we will get our required answer.
Formula used:
xn=dnλD
Complete answer:
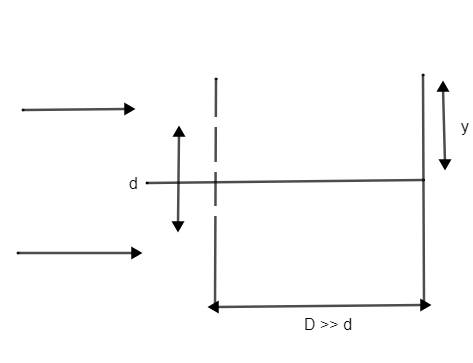
The YSDE arrangement is shown in the figure.
It is given in the question that the value of distance between fringes is given as,
d=10λ
The value of the 8th maxima is given as,
x8=(3xD)
Now we know that formula for the nth maxima is
xn=dnλD...(1)
Where, xn = value of the maxima.
n = 1, 2, 3 ……
λ = wavelength
D = distance between source and SHM.
Now for the 8th number of the maxima,
x8=d8λD
Now substitute all the values given,
⇒3xD=10λ8λD⇒x=1024∴x=2.4
Therefore the value of x is 2.4.
Additional information:
What is the young’s double slit experiment-
Two coherent light sources placed at a small distance apart are used by the young’s double slit experiment, usually only a few orders of magnitude greater than the light wavelength is used.
The double slit experiment by the young’s helped to understand the wavelength theory of the light which is explained using a diagram as seen a screen or photo detector is positioned
away from the slits at a great distance d.
Note:
As an approach to solve this question first we write a formula for the 8th number of maxima. After that we replace value of d by 10λ and x8 by (3xD) which gives us the value of x.
