Question

Consider the trajectory of a golf ball which will be hit with a club, where the initial speed of the ball is $v_0$ , and the angle at which the golf ball leaves the golf club is $\alpha$ . Assume that the horizontal acceleration is $a_{x}=-k{v_{x}}^2$ (where $v_x$ is the horizontal speed) and vertical acceleration is only due to gravity $g$ . Find expressions for $x$ and $y$ positions of a ball as a function of time $t$ , in terms of the initial conditions for the ball $v_0$ , $\alpha$ , and the aerodynamic drag coefficient $k$ .

Answer 1

Hint : The expressions for the $y$ position can be obtained with the help of equations for uniformly accelerated motion. Whereas, the acceleration for the horizontal component is not constant, hence the $x$ position can be obtained from the expressions of velocity and acceleration.

Complete Step By Step Answer:
Consider the ball hit with the initial velocity $v_0$ at an angle of $\alpha$ with the horizontal direction.
Hence, to find the velocity in the horizontal and vertical direction, we need to split the velocity into its respective components as shown in the figure below,

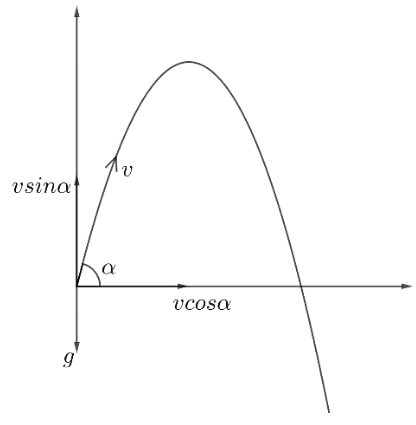
Hence, the vertical component of velocity is ${{v}_{y}}=v\sin \alpha$
And the horizontal component is ${{v}_{x}}=v\cos \alpha$
Now, for the displacement along $x$ -axis,
Let us consider the acceleration given as $a_{x}=-k{v_{x}}^2$
We know that acceleration is defined as change in velocity per unit time.
$\therefore \dfrac{d{{v}_{x}}}{dt}=-k{{v}_{x}}^{2}$
$\therefore \dfrac{d{{v}_{x}}}{{{v}_{x}}^{2}}=-kdt$
Applying integration on both sides,
$\therefore \int{\dfrac{d{{v}_{x}}}{{{v}_{x}}^{2}}}=-k\int{dt}$
$\therefore \dfrac{-1}{{{v}_{x}}}=-kt+c$
To find the value of the constant, we will substitute the boundary points $t=0$ , $v_x=cos\alpha$
$\dfrac{-1}{v\cos \alpha }=-k(0)+c$
$\therefore c=\dfrac{-1}{v\cos \alpha }$
Substituting the value of constant in the equation of velocity,
$\therefore \dfrac{-1}{{{v}_{x}}}=-kt-\dfrac{1}{v\cos \alpha }$
$\therefore \dfrac{1}{{{v}_{x}}}=kt+\dfrac{1}{v\cos \alpha }$
Taking LCM on the right hand side,
$\therefore \dfrac{1}{{{v}_{x}}}=\dfrac{kvt\cos \alpha +1}{v\cos \alpha }$
Taking the reciprocal of the whole equation,
$\therefore {{v}_{x}}=\dfrac{v\cos \alpha }{kvt\cos \alpha +1}$
Now, we know that displacement can be defined as the product of change in velocity and the time,
$\therefore x=\int{{{v}_{x}}dt}$
Substituting the value of velocity in the equation above,
$\therefore x=\int{\dfrac{v\cos \alpha }{kvt\cos \alpha +1}dt}$
Now, let us assume $kvt\cos \alpha +1=z$ for simplification
For time $t=0$ , the value of $z=1$
Differentiating on both sides we get,
$kv\cos \alpha dt=dz$
$\therefore v\cos \alpha dt=\dfrac{dz}{k}$
Substituting these values in the equation of displacement,
$\therefore x=\dfrac{1}{k}\int\limits_{1}^{kvt\cos \alpha +1}{\dfrac{1}{z}dz}$
$\therefore x=\dfrac{1}{k}\left[ \ln z \right]_{1}^{kvt\cos \alpha +1}$
Substituting the boundary values,
$\therefore x=\dfrac{1}{k}[\ln (kvt\cos \alpha +1)-\ln 1]$
$\therefore x=\dfrac{1}{k}\ln (kvt\cos \alpha +1)$
This is the displacement in the horizontal plane.
For the displacement along $y$ -axis,
The initial velocity is $u=v\sin \alpha$
The acceleration only due to gravity is $a=-g$
Here the negative sign shows that the acceleration is in the opposite direction to the gravitational force.
Substituting these values in the equation of uniformly accelerated motion,
$y=ut+\dfrac{1}{2}a{{t}^{2}}$
$\therefore y=v\sin \alpha t-\dfrac{1}{2}g{{t}^{2}}$
This is the displacement in the vertical plane.

Note :
The point to note here, that the acceleration in the horizontal direction is not constant and depends on the value of the velocity. Hence, the equations for uniformly accelerated motion cannot be used here. Also the equation used to find position in vertical direction is used because we are required the positions in terms of time, else we would have used in any of the equations for uniformly accelerated motion.