Question

Consider the statements.

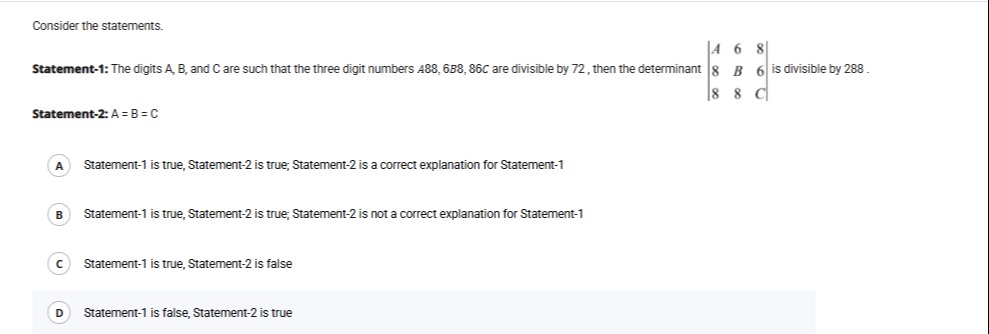
Statement-1: The digits A, B, and C are such that the three digit numbers A88, 6B8, 86C are divisible by 72, then the determinant $\begin{vmatrix} A & 6 & 8 \\ 8 & B & 6 \\ 8 & 8 & C \end{vmatrix}$ is divisible by 288.

Statement-2: A = B = C

• A. Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1
• B. Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1
• C. Statement-1 is true, Statement-2 is false
• D. Statement-1 is false, Statement-2 is true

Answer 1

Answer: (C)

C

Answer 2

Explanation:

1. Divisibility Rules:

   • A number is divisible by 72 if it is divisible by both 8 and 9.

2. Finding A, B, and C:

   • A88 divisible by 8: 88 is divisible by 8, so A can be any digit from 1 to 9 initially.

   • 6B8 divisible by 8: 600 + 10B + 8 must be divisible by 8. Since 608 is divisible by 8, 10B must be divisible by 8, implying B must be a multiple of 4. Possible values for B are 0, 4, 8.

   • 86C divisible by 8: 800 + 60 + C must be divisible by 8. Since 800 is divisible by 8, 60 + C must be divisible by 8. The only digit C for which 60+C is divisible by 8 is C=4.

   • A88 divisible by 9: A + 8 + 8 = A + 16. For A+16 to be divisible by 9, A must be 2.

   • 6B8 divisible by 9: 6 + B + 8 = B + 14. For B+14 to be divisible by 9, B must be 4.

   • 86C divisible by 9: 8 + 6 + C = C + 14. For C+14 to be divisible by 9, C must be 4.

   Therefore, A = 2, B = 4, and C = 4.

3. Evaluating the Determinant:

   Substitute A=2, B=4, C=4 into the determinant:

   $D = \begin{vmatrix} 2 & 6 & 8 \\ 8 & 4 & 6 \\ 8 & 8 & 4 \end{vmatrix}$

   $D = 2(4 \times 4 - 6 \times 8) - 6(8 \times 4 - 6 \times 8) + 8(8 \times 8 - 4 \times 8)$

   $D = 2(16 - 48) - 6(32 - 48) + 8(64 - 32)$

   $D = 2(-32) - 6(-16) + 8(32)$

   $D = -64 + 96 + 256 = 288$

   Since 288 is divisible by 288, Statement-1 is true.

4. Statement-2 Analysis:

   Statement-2 says A = B = C. However, A = 2, B = 4, C = 4. Therefore, Statement-2 is false.

Conclusion: Statement-1 is true, and Statement-2 is false.