Question

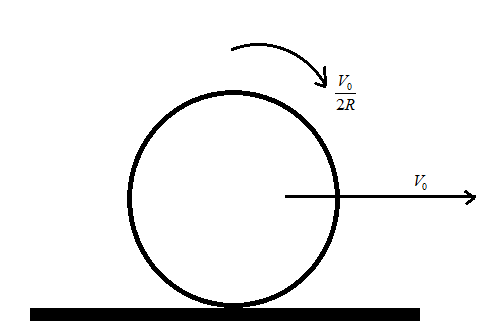
Consider the sphere moving on the horizontal plane at some instant it have line velocity ${V_0}$ and angular velocity about center of mass $\dfrac{{{V_0}}}{{2R}}$ . The translational velocity after the sphere starts pure rolling.

(A) $\dfrac{{5{V_0}}}{7}$
(B) $\dfrac{{6{V_0}}}{7}$
(C) $\dfrac{{3{V_0}}}{4}$
(D) $\dfrac{{3{V_0}}}{5}$

Answer 1

Here, we are supposed to find the velocity of the sphere in translational motion. The sphere has velocity when it is slipping and before the sphere starts rolling. For this we will use the concept of translational and rotational motion.

Complete step by step answer:
here, in the given figure the angular velocity as:
${\omega _0} = \dfrac{{{V_0}}}{{2R}}$
$\Rightarrow {V_0} = 2{\omega _0}R$
$\therefore {V_0} > {\omega _0}R$
Due to slipping of the sphere the friction acts in backward direction as shown below:

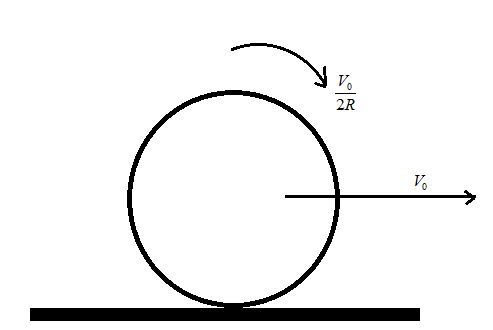
Now here the mass of the sphere is not given then we have to consider mass as $M$ , $f$ is the friction acting in backward direction and $R$ is the radius of the sphere. The moment of inertia along the center of mass is given by:
${I_{CM}} = \dfrac{2}{5}M{R^2}$
Now, for translational motion let $V$ be the translational velocity and it is given by:
$V = {V_0} - at$ …. (Acceleration along the direction of friction force)
$\Rightarrow V = {V_0} - \dfrac{f}{M}t$ …. $(1)$ $\left( {\because f = Ma} \right)$
Now when the sphere starts rolling, the rotational motion and the final angular velocity is given by:
$\omega = {\omega _0} + \alpha t$ …. (Angular acceleration, forward direction)
$\Rightarrow \dfrac{V}{R} = \dfrac{{{V_0}}}{{2R}} + \alpha t$ …. $\left( {\omega = \dfrac{V}{R},{\omega _0} = \dfrac{{{V_0}}}{{2R}}} \right)$ $(2)$
So, we know that torque of the rotational motion is given by:
$\tau = I\alpha$
$\Rightarrow fR = \dfrac{2}{5}M{R^2}\alpha$ …. (Torque is given by the frictional force along the radius)
$\therefore \alpha = \dfrac{{5f}}{{2MR}}$
Put this value in equation $(2)$ , we get:
$\Rightarrow \dfrac{V}{R} = \dfrac{{{V_0}}}{{2R}} + \dfrac{{5f}}{{2MR}}t$
$\Rightarrow V = \dfrac{{{V_0}}}{2} + \dfrac{{5ft}}{{2M}}$ …. $(3)$
On equating $(1)$ and $(3)$
$\Rightarrow {V_0} - \dfrac{f}{M}t = \dfrac{{{V_0}}}{2} + \dfrac{{5ft}}{{2M}}$
On solving this we get
$\Rightarrow \dfrac{1}{2}{V_0} = \dfrac{7}{2}\dfrac{{ft}}{M}$
$\Rightarrow \dfrac{{ft}}{M} = \dfrac{{{V_0}}}{7}$
Now put this value in equation $(1)$ , we get
$\Rightarrow V = {V_0} - \dfrac{{{V_0}}}{7} = \dfrac{{6{V_0}}}{7}$
$\therefore V = \dfrac{{6{V_0}}}{7}$
Hence, we obtained the translational velocity of the sphere when it starts rolling as $\dfrac{{6{V_0}}}{7}$
The correct answer is option B.

Note:
Here, in the given figure we see the sphere is given and the velocity of its center but it has been asked what will be the translational velocity when it starts rolling. For that we considered the slipping motion of the sphere first and then rolling by this we are able to do this problem. Force is acting backward because of forward slipping.