Question
Question: Consider the situation shown in the figure. A spring of spring constant \[400{\text{ }}Nm\]is attach...
Consider the situation shown in the figure. A spring of spring constant 400 Nmis attached at one end to a wedge fixed rigidly with the horizontal part. A 40g mass is released from rest while situated at a height 5cm the curved track. The maximum deformation in the spring is nearly equal to (take g=10m/s2
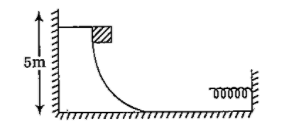
(A) 9.8m
(B) 9.8cm
(C) 0.98m
(D) 0.009km
Solution
Hint In this situation energy from one form is converted into another form hence we can use the conservation of energy theorem with the given values to calculate the spring deformation
Formula Used:
Ki+Pi=Kf+Pf
Complete step by step answer
Since the block is released then initial velocity,u=0and it will follow the curved path and compress the spring till the final velocity of block will be zero after that the spring will regain its position and the block will be thrown back.
Since it is a friction less path, no external force exists. Only conservative forces are present hence you can say that the mechanical energy is conserved between the point of drop till the point of maximum compression of spring.
Ki+Pi=Kf+Pf , where Ki and Kf are the initial and final kinetic energy ---(1)
And Pi and Pf are the initial and final potential energy
We know that potential energy at a height ‘h’ of mass ‘m’ is given by mghwhere g is the acceleration due to gravity and the potential energy stored in the spring is 21kx2 where k is the spring constant and x is the displacement.
Ki=0andKf=0as the initial and final velocities are zero
As you can see that the final potential of block is also zero since its final velocity is zero, but the elastic potential energy will be acting thus
Substituting these in equation (1),
0+mgh=0+21kx2⇒x=k2mgh=4002×0.04×10×5=101m=10cm≅9.8cm
Hence, the correct option is B.
Note
If a string is compressed or stretched then we see that work is done due to spring elasticity, this work done is stored in the spring in the form of elastic potential energy.
