Question

Consider the situation given in Fig. Two cars are moving along road 1 and road 2. Draw the direction of the motion of
(A) Car B as seen from Car A.
(B) Car A as seen from Car B.

Answer 1

Hint
The car B as seen from the car A will be the relative velocity of car B with respect to car A. For that we take the negative of the velocity of car A and do the vector sum with velocity of B. The resultant vector will give the velocity of B with respect to A. Similarly, for A with respect to B, we take the vector sum of velocity of car A and the negative of velocity of car B.
In this solution we will be using the following formula,
$\Rightarrow {\vec V_{AB}} = {\vec V_A} - {\vec V_B}$
where ${\vec V_{AB}}$ is the relative velocity of car A with respect to car B
$\Rightarrow {\vec V_A}$ is velocity of car A and ${\vec V_B}$ is velocity of car B.

Complete step by step answer
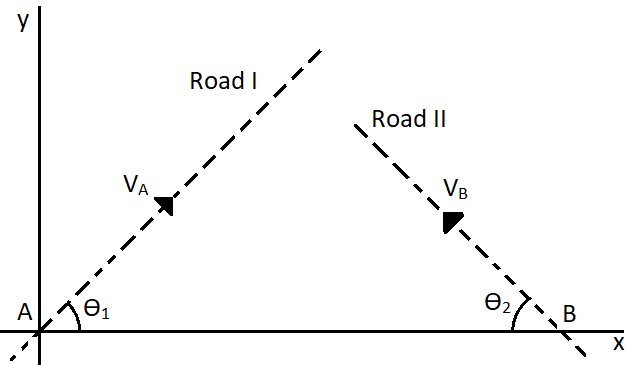
The two cars A and B, as given in the figure, are moving along two roads 1 and 2. The road 1 makes an angle ${\theta _1}$ with the horizontal and rod 2 makes an angle ${\theta _2}$with the horizontal.
Now the velocities of the two cars are taken as, ${\vec V_A}$ and ${\vec V_B}$.
For the first case, the motion of the car B as seen by car A will be given by the direction of the relative velocity vector of the car B with respect to car A. It is denoted by ${\vec V_{BA}}$ and its value is calculated as,
$\Rightarrow {\vec V_{BA}} = {\vec V_B} - {\vec V_A}$
We can write this as the vector sum of the two vectors ${\vec V_B}$ and $- {\vec V_A}$. That is,
$\Rightarrow {\vec V_{BA}} = {\vec V_B} + \left( { - {{\vec V}_A}} \right)$
Therefore we can draw the diagram as,

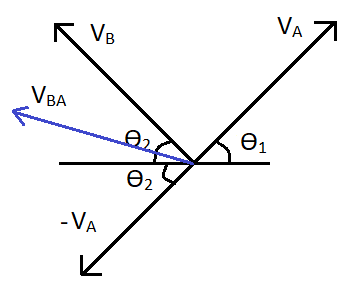
The blue line gives the direction of ${\vec V_{BA}}$. So that will be the direction that the car B moves as seen by car A.
Similarly for the second case, the motion of the car A as seen by car B will be given by the direction of the relative velocity vector of the car A with respect to car B. It is denoted by ${\vec V_{AB}}$ and its value is calculated as,
$\Rightarrow {\vec V_{AB}} = {\vec V_A} - {\vec V_B}$
We can write this as the vector sum of the two vectors ${\vec V_A}$ and $- {\vec V_B}$. That is,
$\Rightarrow {\vec V_{AB}} = {\vec V_A} + \left( { - {{\vec V}_B}} \right)$
Therefore we can draw the diagram as,

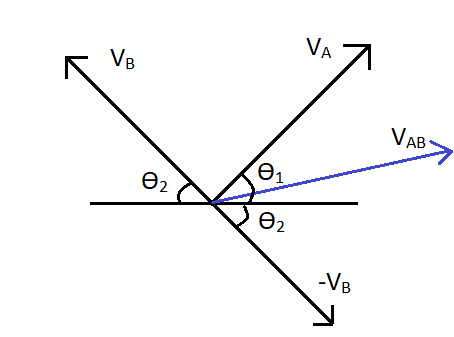
The blue line gives the direction of ${\vec V_{AB}}$. So that will be the direction that the car A moves as seen by car B.

Note
The relative velocity of one body A with respect to another body B is the velocity of A as seen by an observer from the rest frame in B. In case of one dimensional motion, the relative velocity can be calculated simply by adding or subtracting according to the direction of motion. For two dimensional motion, the relative velocity is found by the parallelogram law of the vectors.