Question
Question: Consider the situation as shown in figure below. The acceleration of block of mass m is ...
Consider the situation as shown in figure below. The acceleration of block of mass m is
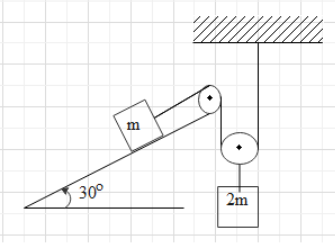
Solution
We have given a diagram in which we have to find the acceleration for the block of mass m. Now there are two blocks of mass m and 2m respectively and there will be some force acting on it. So we will be redrawing the diagram and labelling the force on mass m and 2m. Then by balancing the forces we can find the acceleration of the block of mass m.
Complete answer:
Let us first redraw the given diagram to show forces acting on mass m and 2m.
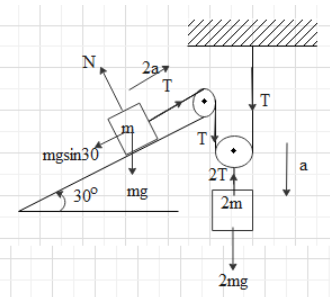
If T is the tension in the string attached to the block of mass m, then the tension in the string attached to block 2m will be 2T. As we can see there are two components of T which is balancing the string attached to mass 2m.
Now if we consider block 2m and if it is moving with acceleration a downward, then the forces on it will be the downward gravitational pull 2mg, upward tension i.e. 2T and the force due to its motion which is 2ma. Neglecting the friction between the surfaces and considering the pulley and string massless, if we balance the forces we get
