Question

Consider the shown circuit if each battery has zero internal resistance, then potential difference across point $C$ and $D$ is

A. $2{\text{ }}V\:$
B. $3{\text{ }}V\:$
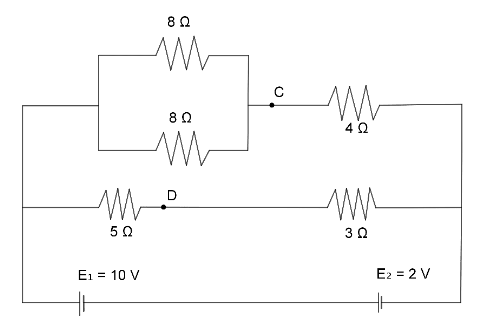
C. $1.5{\text{ }}V\:$
D. $4{\text{ }}V$

Answer 1

We will firstly find the net potential difference of the circuit. Then, we will consider the currents through the different arms of the circuit. Then we will use the basic concepts of potential drop and potential lift. Finally, we will evaluate the potential difference between the two points.

Formulae used:
Equivalent resistance of resistances in series:
${R_{Series}}{\text{ }} = {\text{ }}{R_1}{\text{ }} + {\text{ }}{R_2}{\text{ }} + {\text{ }}.......{\text{ }} + {\text{ }}{R_n}$
Equivalent resistance of resistances in parallel:
$\dfrac{1}{{{R_{Parallel}}}}{\text{ }} = {\text{ }}\dfrac{1}{{{R_1}}}{\text{ }} + {\text{ }}\dfrac{1}{{{R_2}}}{\text{ }} + {\text{ }}......{\text{ }} + {\text{ }}\dfrac{1}{{{R_n}}}$
Current through a circuit:
$I{\text{ }} = {\text{ }}\dfrac{V}{R}$
Potential through a circuit:
$V{\text{ }} = {\text{ }}IR$

Complete step by step answer:
Since the polarity of both the cells are same thus the net potential will be the sum of the two potentials. Thus,
${E_o}{\text{ }} = {\text{ }}{E_1}{\text{ }} + {\text{ }}{E_2}$
Substituting the values, we get
${E_o}{\text{ }} = {\text{ }}10{\text{ }}V{\text{ }} + {\text{ }}2{\text{ }}V$
Thus, we get
${E_o}{\text{ }} = {\text{ }}12{\text{ }}V$
Let us say current $I$ be the net flowing current of the combination of the cells.And the current through the other arms be ${I_1}$ and ${I_2}$.
The resistances in the circuit are
${R_1}{\text{ }} = {\text{ }}8{\text{ }}\Omega$
$\Rightarrow {R_2}{\text{ }} = {\text{ }}8{\text{ }}\Omega$
$\Rightarrow {R_3}{\text{ }} = {\text{ }}4{\text{ }}\Omega$
$\Rightarrow {R_4}{\text{ }} = {\text{ }}5{\text{ }}\Omega$
$\Rightarrow {R_5}{\text{ }} = {\text{ }}3{\text{ }}\Omega$
Now, the net resistance of the secondary circuit is,
$\dfrac{1}{{{R_{\operatorname{Sec} }}}}{\text{ }} = {\text{ }}\dfrac{1}{{{R_1}}}{\text{ }} + {\text{ }}\dfrac{1}{{{R_2}}}$
Substituting the value, we get
$\dfrac{1}{{{R_{\operatorname{Sec} }}}}{\text{ }} = {\text{ }}\dfrac{1}{8}{\text{ }} + {\text{ }}\dfrac{1}{8}$

After further evaluation, we get
${R_{\operatorname{Sec} }}{\text{ }} = {\text{ }}4{\text{ }}\Omega$
Then, the net resistance of the upper arm is
${R_{Up}}{\text{ }} = {\text{ }}(4{\text{ }} + {\text{ }}4){\text{ }}\Omega {\text{ }} = {\text{ }}8{\text{ }}\Omega$
Now, the net resistance of the lower arm is,
${{\text{R}}_{{\text{Low}}}}{\text{ = (5 + 3) }}\Omega {\text{ = 8 }}\Omega$
Now, the value of current
${I_1}{\text{ }} = {\text{ }}\dfrac{{{E_o}}}{{{R_{Low}}}}$
Substituting the values, we get
${I_1}{\text{ }} = {\text{ }}\dfrac{{12}}{8}{\text{ }} = {\text{ }}\dfrac{3}{2}$
Thus, the potential drop across point $D$ is,
${V_D}{\text{ }} = {\text{ }}{E_o}{\text{ }} - {\text{ }}{I_1}{R_4}$
Substituting the value, we get

\Rightarrow {V_D}{\text{ }} = {\text{ }}\dfrac{9}{2}{\text{ }}V$$ Similarly, the value of current ${I_2}{\text{ }} = {\text{ }}\dfrac{{{E_o}}}{{{R_{Up}}}}$ Substituting the values, we get ${I_2}{\text{ }} = {\text{ }}\dfrac{{12}}{8}{\text{ }} = {\text{ }}\dfrac{3}{2}$ Thus, the potential drop across point $C$ is, $${V_C}{\text{ }} = {\text{ }}{E_o}{\text{ }} - {\text{ }}{I_2}{R_{\operatorname{Sec} }}$$ Substituting the value, we get $${V_C}{\text{ }} = {\text{ }}12{\text{ }} - {\text{ 4 }} \times {\text{ }}\dfrac{3}{2}{\text{ }} \\\ \Rightarrow {V_C}{\text{ }}= {\text{ 6 }}V$$ Thus, Potential Difference across $CD$ is, ${V_{CD}}{\text{ }} = {\text{ }}{V_D}{\text{ }} - {\text{ }}{V_C}$ Putting in the evaluated values, we get $\therefore {V_{CD}} = 1.5{\text{ }}V$ **Thus, the correct answer is option C.** **Note:** Students often make errors in calculating the net resistances. Thus, they have to be very much cautious in using the suitable formula for the net resistance. The students must also be careful while evaluating the potential drop across a resistor as they misinterpret it by calculating just the current multiplied by the resistance value but forget that it is actually the difference between the net potential of the circuit and the potential across the resistor. Only the resistor(s) in the path of the current up till the point for which we need the potential drop is to be considered for the calculation.