Question

Consider the set $P = \{1, 2, \frac{\pi}{4}, \frac{\pi}{2}, 0\}$ and let Q be the set of all the values of t for which the matrix $A = \begin{bmatrix} e^t & e^{-t}cost & e^{-t}sint \\ e^t & -e^{-t}cost - e^{-t}sint & -e^{-t}sint + e^{-t}cost \\ e^t & 2e^{-t}sint & -2e^{-t}cost \end{bmatrix}$ is invertible, then the number of elements in $P \cap Q$ is equal to

Answer 1

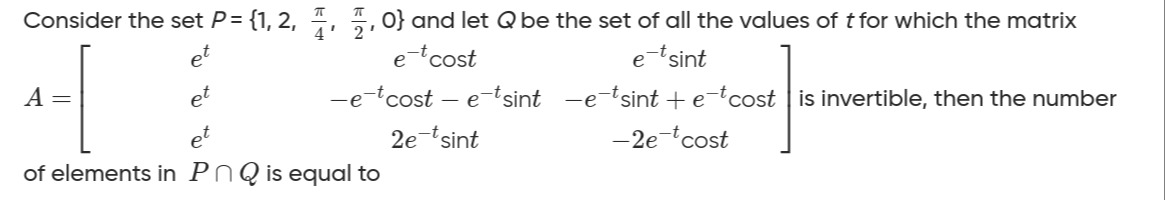
5

Answer 2

To determine the number of elements in $P \cap Q$, we first need to define the set Q.

The set Q consists of all values of 't' for which the matrix A is invertible. A matrix is invertible if and only if its determinant is non-zero. So, we need to find 't' such that $\det(A) \neq 0$.

The given matrix is: $A = \begin{bmatrix} e^t & e^{-t}cost & e^{-t}sint \\ e^t & -e^{-t}cost - e^{-t}sint & -e^{-t}sint + e^{-t}cost \\ e^t & 2e^{-t}sint & -2e^{-t}cost \end{bmatrix}$

Step 1: Calculate the determinant of A.

We can factor out $e^t$ from the first column ($C_1$), $e^{-t}$ from the second column ($C_2$), and $e^{-t}$ from the third column ($C_3$).

$\det(A) = e^t \cdot e^{-t} \cdot e^{-t} \begin{vmatrix} 1 & cost & sint \\ 1 & -cost - sint & -sint + cost \\ 1 & 2sint & -2cost \end{vmatrix}$

$\det(A) = e^{-t} \begin{vmatrix} 1 & cost & sint \\ 1 & -(cost + sint) & -(sint - cost) \\ 1 & 2sint & -2cost \end{vmatrix}$

Step 2: Simplify the determinant using row operations.

Apply the operations: $R_2 \rightarrow R_2 - R_1$ and $R_3 \rightarrow R_3 - R_1$.

$\det(A) = e^{-t} \begin{vmatrix} 1 & cost & sint \\ 1-1 & -(cost + sint) - cost & -(sint - cost) - sint \\ 1-1 & 2sint - cost & -2cost - sint \end{vmatrix}$

$\det(A) = e^{-t} \begin{vmatrix} 1 & cost & sint \\ 0 & -2cost - sint & -2sint + cost \\ 0 & 2sint - cost & -2cost - sint \end{vmatrix}$

Step 3: Expand the determinant along the first column.

$\det(A) = e^{-t} \cdot 1 \cdot \left( (-2cost - sint)(-2cost - sint) - (-2sint + cost)(2sint - cost) \right)$

$\det(A) = e^{-t} \left( (2cost + sint)^2 - (-(2sint - cost))(2sint - cost) \right)$

$\det(A) = e^{-t} \left( (2cost + sint)^2 + (2sint - cost)^2 \right)$

Step 4: Expand and simplify the trigonometric terms.

Let's expand the squares:

$(2cost + sint)^2 = (2cost)^2 + (sint)^2 + 2(2cost)(sint) = 4cos^2t + sin^2t + 4sintcost$

$(2sint - cost)^2 = (2sint)^2 + (cost)^2 - 2(2sint)(cost) = 4sin^2t + cos^2t - 4sintcost$

Now, sum these two expressions:

$(4cos^2t + sin^2t + 4sintcost) + (4sin^2t + cos^2t - 4sintcost)$ $= 4cos^2t + cos^2t + sin^2t + 4sin^2t + 4sintcost - 4sintcost$ $= 5cos^2t + 5sin^2t$ $= 5(cos^2t + sin^2t)$

Using the identity $cos^2t + sin^2t = 1$: $= 5(1) = 5$

Step 5: Substitute the simplified expression back into the determinant.

$\det(A) = e^{-t} \cdot 5 = 5e^{-t}$

Step 6: Determine the set Q.

For the matrix A to be invertible, $\det(A) \neq 0$.

So, $5e^{-t} \neq 0$.

Since the exponential function $e^{-t}$ is always positive for any real value of $t$ ($e^{-t} > 0$), $5e^{-t}$ will always be positive and thus never equal to zero.

Therefore, the matrix A is invertible for all real values of $t$.

This means the set $Q = \mathbb{R}$ (the set of all real numbers).

Step 7: Find the number of elements in $P \cap Q$.

The given set $P = \{1, 2, \frac{\pi}{4}, \frac{\pi}{2}, 0\}$.

The set $Q = \mathbb{R}$.

The intersection $P \cap Q$ consists of all elements that are in both P and Q. Since all elements in P are real numbers, every element of P is also an element of Q.

Thus, $P \cap Q = P$.

The elements of $P \cap Q$ are $\{1, 2, \frac{\pi}{4}, \frac{\pi}{2}, 0\}$.

The number of elements in $P \cap Q$ is 5.

The final answer is $\boxed{5}$.