Question

Consider the relation $4{{l}^{2}}-5{{m}^{2}}+6l+1=0$ , where l,m belongs to a set of real numbers . tangent PA and PB are drawn to the above fixed circle from the points P on the line x + y – 1 = 0. Then the chord of contact AP passes through the fixed point.
(a) $\left( \dfrac{1}{2},-\dfrac{5}{2} \right)$
(b)$\left( \dfrac{1}{3},\dfrac{4}{3} \right)$
(c)$\left( -\dfrac{1}{2},\dfrac{3}{2} \right)$
(d) none of these

Answer 1

Firstly, we will find the values of f, g and c by comparing relations we get from $\dfrac{\left| -gl=mf+1 \right|}{\sqrt{{{l}^{2}}+{{m}^{2}}}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ and $4{{l}^{2}}-5{{m}^{2}}+6l+1=0$. Then we will find the equation of the circle by putting values of f and g and c. Then using the property of concurrency that a single point will satisfy the lines, we will find the point using the equation of lines.

Complete step-by-step answer:
Let consider the general equation of the circle be ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ ….. ( i )
So, we know that if we have line lx + my +1 = 0 will touch circle if the length of perpendicular from the centre ( -g, -f ) of the circle on the line is equal to its radius that is,
$\dfrac{\left| -gl=mf+1 \right|}{\sqrt{{{l}^{2}}+{{m}^{2}}}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
Or, using cross multiplication we get
$\left| -gl=mf+1 \right|=\sqrt{{{g}^{2}}+{{f}^{2}}-c}\times \sqrt{{{l}^{2}}+{{m}^{2}}}$
Squaring both sides we get
${{\left( -gl=mf+1 \right)}^{2}}=\left( {{g}^{2}}+{{f}^{2}}-c \right)\times \left( {{l}^{2}}+{{m}^{2}} \right)$
Solving brackets on both sides we get
${{g}^{2}}{{l}^{2}}+{{m}^{2}}{{f}^{2}}+1-2glmf+2mf-2gl={{g}^{2}}{{l}^{2}}+{{g}^{2}}{{m}^{2}}+{{f}^{2}}{{l}^{2}}+{{f}^{2}}{{m}^{2}}-c{{l}^{2}}-c{{m}^{2}}$
Taking common terms out from the equation, we get
$(c-{{f}^{2}}){{l}^{2}}+(c-{{g}^{2}}){{m}^{2}}-2gl-2fm+2fglm+1=0$ ….( ii )
In question we have relation, $4{{l}^{2}}-5{{m}^{2}}+6l+1=0$…..( iii )
Comparing equation ( ii ) and ( iii ), we get
$(c-{{f}^{2}})=4,(c-{{g}^{2}})=-5,-2g=6,-2f=0,2fg=0,$
Solving further, we get -2f = 0, -2g = 6 and ( c – 0 ) = 4
So, f = 0, g = -3 and c = 4
Substituting values in equation ( i ), we get
Equation of circle as, ${{x}^{2}}+{{y}^{2}}-6x+4=0$

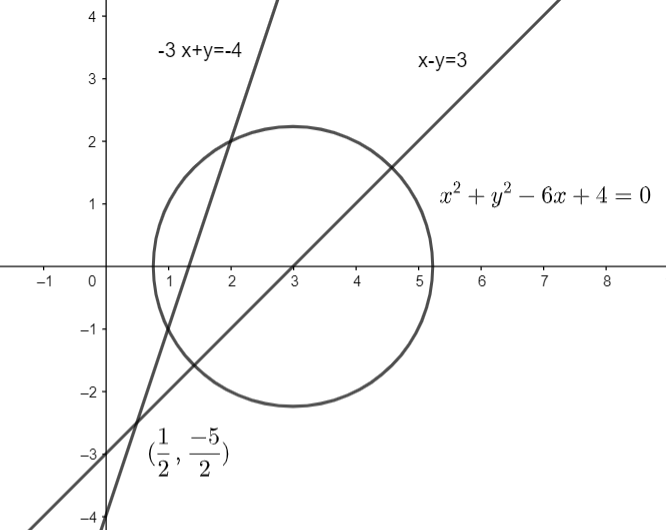
Now, any point on the line x + y – 1 = 0 is ( t, 1 – t), where t belongs to a set of real numbers.
The chord of contact with respect to point ( t, 1 – t) of circle is tx + y(1 - t) – 3(t + x) + 4 = 0
Or, t( x – y -3 ) + ( -3x + y + 4 ) = 0, which is concurrent at the point of intersection of the lines x - y - 3 = 0 and -3x + y + 4 = 0 for all values of t.
So, common point ( x, y ) satisfying lines x - y - 3 = 0 and -3x + y + 4 = 0, will be
-3x + ( x -3 ) + 4 = 0
On solving, we get
-2x = -1
$x=\dfrac{1}{2}$
Putting value of $x=\dfrac{1}{2}$ in x - y – 3 = 0, we get
$\dfrac{1}{2}-y-3=0$
On solving, we get
$y=-\dfrac{5}{2}$
So, the lines are concurrent at $\left( \dfrac{1}{2},-\dfrac{5}{2} \right)$.

So, the correct answer is “Option (a)”.

Note: To solve such questions, always remember that general equation of circle is of form ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ also, if we have line lx + my +1 = 0 will touch circle if the length of perpendicular from the centre ( -g, -f ) of the circle on the line is equal to its radius that is, $\dfrac{\left| -gl=mf+1 \right|}{\sqrt{{{l}^{2}}+{{m}^{2}}}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$. Concurrent lines are lines in a plane which meet at a single point, so that single point will satisfy all the equations of lines which are concurrent at that point.