Question
Question: Consider the region $R=\{(x, y): x^2 + y^2 \leq 100, \sin(x+y) > 0\}$. What is the area of $R$?...
Consider the region R={(x,y):x2+y2≤100,sin(x+y)>0}. What is the area of R?
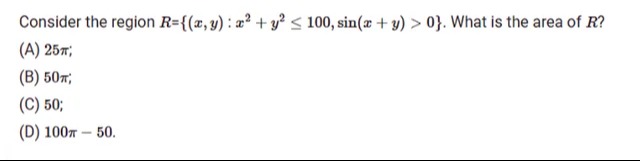
25π
50π
50
100π−50
50π
Solution
The problem asks for the area of the region R={(x,y):x2+y2≤100,sin(x+y)>0}.
Let's analyze the two conditions defining the region R:
-
x2+y2≤100: This inequality describes a closed disk centered at the origin (0,0) with a radius of r=100=10. Let's call this disk D. The total area of this disk is AD=πr2=π(10)2=100π.
-
sin(x+y)>0: This inequality specifies which part of the disk we are interested in. The sine function is positive when its argument lies in the intervals (2nπ,(2n+1)π) for any integer n. So, we need x+y∈(2nπ,(2n+1)π). This means the region R consists of parts of the disk D that fall within these parallel strips defined by 2nπ<x+y<(2n+1)π.
To find the area of R, we can use a symmetry argument. Let f(x,y)=sin(x+y). The region D (the disk x2+y2≤100) is symmetric with respect to the origin. This means that if a point (x,y) is in D, then its antipodal point (−x,−y) is also in D.
Now let's examine the condition sin(x+y)>0: Consider a point (x,y) in R. By definition, (x,y)∈D and sin(x+y)>0. Now consider the antipodal point (−x,−y). Since (x,y)∈D and D is symmetric about the origin, (−x,−y) is also in D. Let's evaluate sin at this new point: sin((−x)+(−y))=sin(−(x+y)) Using the trigonometric identity sin(−θ)=−sin(θ), we get: sin(−(x+y))=−sin(x+y).
Since we know that sin(x+y)>0 for (x,y)∈R, it follows that for the antipodal point (−x,−y), sin((−x)+(−y))=−sin(x+y)<0.
Let R+ be the region where sin(x+y)>0 within the disk D. So R=R+. Let R− be the region where sin(x+y)<0 within the disk D. Let R0 be the region where sin(x+y)=0 within the disk D. This corresponds to lines x+y=kπ for integers k. The area of a finite set of lines is zero. Therefore, the total area of the disk D is Area(D)=Area(R+)+Area(R−).
The mapping T(x,y)=(−x,−y) is a rotation by 180∘ about the origin. This transformation preserves area. We showed that if (x,y)∈R+, then T(x,y)=(−x,−y)∈R−. Similarly, if (x,y)∈R−, then T(x,y)=(−x,−y)∈R+. This establishes a one-to-one, area-preserving correspondence between the points in R+ and the points in R−. Therefore, Area(R+)=Area(R−).
Since Area(D)=Area(R+)+Area(R−) and Area(R+)=Area(R−), we have: Area(D)=2×Area(R+) 100π=2×Area(R+) Area(R+)=2100π=50π.
The area of region R is 50π.
